Question

Find the real solution of ${{\tan }^{-1}}\sqrt{x\left( x+1 \right)}+{{\sin }^{-1}}\sqrt{{{x}^{2}}+x+1}=\dfrac{\pi }{2}$.

Answer 1

Hint: For this problem we need to calculate the real solution of the given equation. For this we are going to use the inverse trigonometric formulas. First, we will consider the value ${{\tan }^{-1}}\sqrt{x\left( x+1 \right)}$ and assume it to be $\theta $ and calculate the value of $\tan \theta $. From the value of $\tan \theta $ we will construct a triangle and find the value of $\theta $ in terms of ${{\cos }^{-1}}$. Now we will substitute this value as ${{\tan }^{-1}}\sqrt{x\left( x+1 \right)}$ in the given equation. Here we can use the inverse trigonometric formula which is ${{\sin }^{-1}}\theta +{{\cos }^{-1}}\theta =\dfrac{\pi }{2}$. From this we can equate the values which are in trigonometric ratios and simplify them to get the required result.

Complete step by step solution:
Given equation ${{\tan }^{-1}}\sqrt{x\left( x+1 \right)}+{{\sin }^{-1}}\sqrt{{{x}^{2}}+x+1}=\dfrac{\pi }{2}$.
Considering the value ${{\tan }^{-1}}\sqrt{x\left( x+1 \right)}$.
Let ${{\tan }^{-1}}\sqrt{x\left( x+1 \right)}=\theta $
Applying $\tan $ function on both sides of the above equation, then we will get
$\tan \theta =\tan \left( {{\tan }^{-1}}\left( \sqrt{x\left( x+1 \right)} \right) \right)$
The functions $\tan $ and ${{\tan }^{-1}}$ are get cancelled to each other, then the above equation is modified as
$\tan \theta =\sqrt{x\left( x+1 \right)}$
We have the definition of the $\tan \theta $ as $\dfrac{\text{Opposite side to }\theta }{\text{Adjacent side to }\theta }$. So, we can construct a triangle as

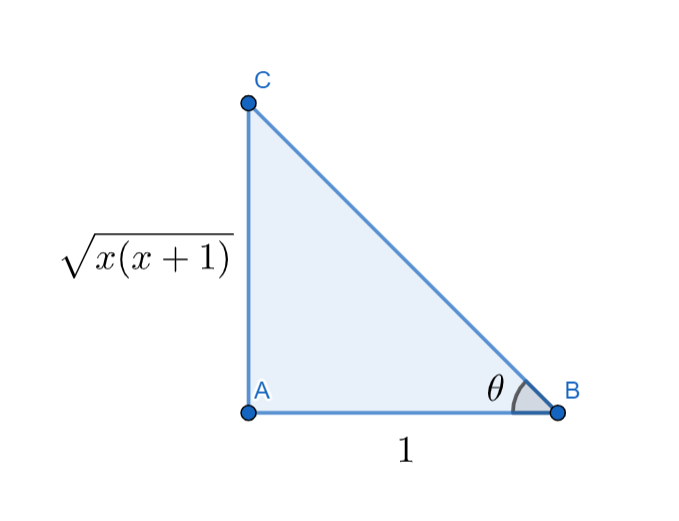
From Pythagoras theorem we can write the value of hypotenuse as
$\begin{align}
  & hyp=\sqrt{{{1}^{2}}+{{\left( \sqrt{x\left( x+1 \right)} \right)}^{2}}} \\
 & \Rightarrow hyp=\sqrt{1+{{x}^{2}}+x} \\
 & \Rightarrow hyp=\sqrt{{{x}^{2}}+x+1} \\
\end{align}$
Now the value of $\cos \theta $ will be
$\begin{align}
  & \cos \theta =\dfrac{\text{Adjacent side to }\theta }{\text{Hypotenuse}} \\
 & \Rightarrow \cos \theta =\dfrac{1}{\sqrt{{{x}^{2}}+x+1}} \\
\end{align}$
From the above equation the value of $\theta $ will be
$\theta ={{\cos }^{-1}}\left( \dfrac{1}{\sqrt{{{x}^{2}}+x+1}} \right)$
Bur we have assumed that ${{\tan }^{-1}}\sqrt{x\left( x+1 \right)}=\theta $. From both these values, we can write
${{\tan }^{-1}}\sqrt{x\left( x+1 \right)}={{\cos }^{-1}}\left( \dfrac{1}{\sqrt{{{x}^{2}}+x+1}} \right)$
Substituting this value in the given equation ${{\tan }^{-1}}\sqrt{x\left( x+1 \right)}+{{\sin }^{-1}}\sqrt{{{x}^{2}}+x+1}=\dfrac{\pi }{2}$, then we will get
${{\cos }^{-1}}\left( \dfrac{1}{\sqrt{{{x}^{2}}+x+1}} \right)+{{\sin }^{-1}}\left( \sqrt{{{x}^{2}}+x+1} \right)=\dfrac{\pi }{2}$
We have the inverse trigonometric formula which is ${{\sin }^{-1}}\theta +{{\cos }^{-1}}\theta =\dfrac{\pi }{2}$. By considering this formula, from the above equation we can write
$\dfrac{1}{\sqrt{{{x}^{2}}+x+1}}=\sqrt{{{x}^{2}}+x+1}$
Simplifying the above equation by cross multiplication, then we will have
${{x}^{2}}+x+1=1$
Subtracting $1$ on both sides and taking $x$ as common from the terms ${{x}^{2}}+x$, then the above equation is modified as
$\begin{align}
  & x\left( x+1 \right)+1-1=1-1 \\
 & \Rightarrow x\left( x+1 \right)=0 \\
\end{align}$
Equating each term individually, then we will get
$\begin{align}
  & x=0\text{ or }x+1=0 \\
 & \Rightarrow x=0\text{ or }x=-1 \\
\end{align}$
Hence the real solution for the given equation ${{\tan }^{-1}}\sqrt{x\left( x+1 \right)}+{{\sin }^{-1}}\sqrt{{{x}^{2}}+x+1}=\dfrac{\pi }{2}$ is $x=0,-1$.

Note: For this problem we can also consider the term ${{\sin }^{-1}}\left( \sqrt{{{x}^{2}}+x+1} \right)$ and convert it into ${{\cot }^{-1}}$ by constructing a triangle and applying some basic trigonometric definitions and Pythagoras theorem. After that substitute the converted value in the given equation and use the inverse trigonometric formula ${{\tan }^{-1}}x+{{\cot }^{-1}}x=\dfrac{\pi }{2}$ and follow the above procedure to calculate the required result.