Question

Find the ratio of geometrical isomers in $\left[ {M{{\left( {AA} \right)}_2}{b_2}} \right]$ and optical isomers of $\left[ {M{{\left( {AA} \right)}_3}} \right]$.
A: $1$
B: $2$
C: $1.5$
D: $2.5$

Answer 1

Hint:Isomers are the chemical compounds that have the same molecular formula, that is they have the same number of atoms of each element but their arrangement is different. Isomers may or may not have the same physical and chemical properties.

Complete step by step answer:
In this question we have to find the ratio of geometrical isomers in $\left[ {M{{\left( {AA} \right)}_2}{b_2}} \right]$ and optical isomers of $\left[ {M{{\left( {AA} \right)}_3}} \right]$. Isomers are the chemical compounds that have the same molecular formula, that is they have the same number of atoms of each element but their arrangement is different. Isomers may or may not have the same physical and chemical properties.
Geometric isomers are of two types, cis and trans. If the functional groups are on the same side of the carbon chain the prefix cis is used and if the functional groups are on the opposite side of the carbon chain prefix trans is used. Following figure shows cis and trans molecules:

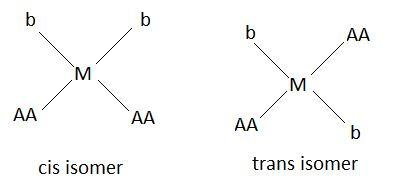
This picture shows geometric isomers of $\left[ {M{{\left( {AA} \right)}_2}{b_2}} \right]$. Therefore $\left[ {M{{\left( {AA} \right)}_2}{b_2}} \right]$ molecule has two geometric isomers.
Optical isomers are those isomers which contain the same number of atoms of each element but have different spatial arrangement. These arrangements have non-superimposable mirror images. These non-superimposable images are called enantiomers. Following figure shows optical isomers of $\left[ {M{{\left( {AA} \right)}_3}} \right]$:

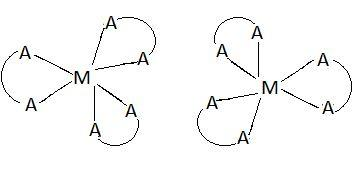
These are the two possible optical isomers of $\left[ {M{{\left( {AA} \right)}_3}} \right]$. These are non-superimposable mirror images of each other. This means there are two optical isomers of $\left[ {M{{\left( {AA} \right)}_3}} \right]$.
We have to find the ratio of geometric isomers of $\left[ {M{{\left( {AA} \right)}_2}{b_2}} \right]$ and optical isomers of $\left[ {M{{\left( {AA} \right)}_3}} \right]$. So,
Ratio$ = \dfrac{{{\text{geometric isomers of }}\left[ {M{{\left( {AA} \right)}_2}{b_2}} \right]}}{{{\text{optical isomers of }}\left[ {M{{\left( {AA} \right)}_3}} \right]}}$
There are two geometric isomers of $\left[ {M{{\left( {AA} \right)}_2}{b_2}} \right]$ and two optical isomers of $\left[ {M{{\left( {AA} \right)}_3}} \right]$. Substituting these values in the above equation to find the ratio,
Ratio$ = \dfrac{2}{2} = 1$
Therefore the ratio is one and the correct answer is option A.


Note:
Optical isomers can rotate planes of polarized light. Isomers that rotate planes of polarized light to right are called dextrorotatory and the isomers that can rotate planes of polarized light to the left are called levorotatory.