Question

Find the range and domain of the function $f\left( x \right)=\sqrt{9-{{x}^{2}}}$.

Answer 1

Hint: We recall the ideas of domain from where the functions take the input value and range where the function collects the output. We use the knowledge that the square root functions can only have input from a positive real number set $\left( {{\mathsf{\mathbb{R}}}^{+}} \right)$ and return positive real numbers. So the expression inside the square root $\left( 9-{{x}^{2}} \right)$ has to be positive.

Complete step by step answer:
 Before going to the problem we need to know what is the range and domain of the function.

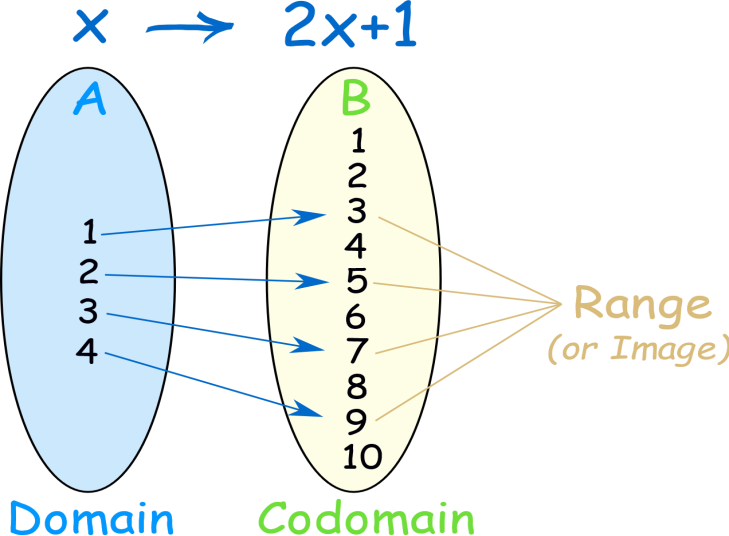
In the above image, we can say that the set $A$ is the Domain of the function $f\left( x \right)=2x+1$ and set $B$ is the codomain of the function $f\left( x \right)=2x+1$ and the set of elements that get pointed to in $B$(the actual values produced by the function) are the Range of the function. Hence, we can write
1. Domain: $\left\{ 1,2,3,4 \right\}$
2. Codomain: $\left\{ 1,2,3,4,5,6,7,8,9,10 \right\}$
3. Range: $\left\{ 3,5,7,9 \right\}$
Now let us see how to find the range and domain of the function.
Generally, the functions are defined as an expression of $x$. So, the domain of a function means finding the values of $x$ for which the function is defined and gives a real value as an output. Based on the expressions involved in the function we will assume the conditions to get the values of $x$.
Finding the range of function: In this process we will assume $f\left( x \right)=y$ and find the value of $x$in terms of $y$. Now substitute the value of $x$ in its range and find the limits of $y$. Now the limits of $y$ is the range of the function.
For this problem we take the condition to find the domain of the given function $f\left( x \right)=\sqrt{9-{{x}^{2}}}$ as $9-{{x}^{2}}\ge 0$ and calculate the values $x$ where function is defined and given a real number as output.
For the range of the function, we will find the values of the function for the maximum and minimum values of $x$ in its range.
Given that, $f\left( x \right)=\sqrt{9-{{x}^{2}}}$
The function has expression in terms of $x$ as $\sqrt{9-{{x}^{2}}}$, now the domain of the function is
$\begin{align}
& 9-{{x}^{2}}\ge 0 \\
&\Rightarrow {{3}^{2}}-{{x}^{2}}\ge 0
\end{align}$
Now using the formula ${{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)$ in the above expression, then
$\begin{align}
& \left( 3+x \right)\left( 3-x \right)\ge 0 \\
&\Rightarrow 3+x\ge 0\text{ or }\left( 3-x \right)\ge 0 \\
&\Rightarrow x\ge -3\text{ or }x\le 3 \\
&\Rightarrow -3\le x\le 3
\end{align}$
Hence the domain of the function is $x\in \left[ -3,3 \right]$.
The range of the function is lies between the maximum value of $y$ and minimum value of $y$
For maximum and minimum value of $y$ substitute the maximum and minimum values of $x$ in its range.
The maximum value of $x$ in $\left[ -3,3 \right]$ is ${{x}_{\max }}=3$ and the minimum value of $x$ in $\left[ -3,3 \right]$ is ${{x}_{\min }}=0$
Now the maximum and minimum value of $y$ are
$\begin{align}
& y=\sqrt{9-{{x}^{2}}_{\max }} \\
& =\sqrt{9-{{3}^{2}}} \\
& =0
\end{align}$ $\begin{align}
& y=\sqrt{9-{{x}_{\min }}^{2}} \\
& =\sqrt{9-{{0}^{2}}} \\
& =3
\end{align}$
Hence the range of $y$ is $\left[ 0,3 \right]$

So, the domain and range of the function $f\left( x \right)=\sqrt{9-{{x}^{2}}}$ is $\left[ -3,3 \right]$ and $\left[ 0,3 \right]$.

Note: We can find the range of the functions from graphs after finding the domain of the function. After finding the domain it’s better to verify the output of the function by substituting the random values in the domain. And check if the output lies in range or not.