Question

Find the principal value of \[se{{c}^{-1}}\left( 2\sin \left( \dfrac{3\pi }{4} \right) \right)\]

Answer 1

Hint: First of all, consider the principal value of \[se{{c}^{-1}}\left( 2\sin \left( \dfrac{3\pi }{4} \right) \right)\] as y. Now, write \[\dfrac{3\pi }{4}=\pi -\dfrac{\pi }{4}\] and use \[\sin \left( \pi -\theta \right)=\sin \theta \] and table of trigonometric ratios to find the value of \[2\sin \dfrac{3\pi }{4}\]. Now, take sec on both the sides and use the trigonometric ratios table to find the principal value of the given expression.

Complete step-by-step answer:
Here, we have to find the principal value of \[se{{c}^{-1}}\left( 2\sin \left( \dfrac{3\pi }{4} \right) \right)\]. Let us take the principal value of \[se{{c}^{-1}}\left( 2\sin \left( \dfrac{3\pi }{4} \right) \right)\] as y. So, we get,
\[y=se{{c}^{-1}}\left( 2\sin \left( \dfrac{3\pi }{4} \right) \right)\]
Now by taking sec on both sides of the above equation, we get,
\[secy=sec\left[ se{{c}^{-1}}\left( 2\sin \left( \dfrac{3\pi }{4} \right) \right) \right]\]
We know that \[sec\left( se{{c}^{-1}}x \right)=x\]. By using this in the RHS of the above equation, we get,
\[secy=2\sin \left( \dfrac{3\pi }{4} \right)\]
We can also write the above equation as
\[secy=2\sin \left( \pi -\dfrac{\pi }{4} \right)\]
We know that \[\sin \left( \pi -\theta \right)=\sin \theta \]. By using this in the above equation, we get,
\[secy=2\sin \left( \dfrac{\pi }{4} \right).....\left( i \right)\]
Now, let us find the value at which \[\sin \left( \dfrac{\pi }{4} \right)\] from the table below.

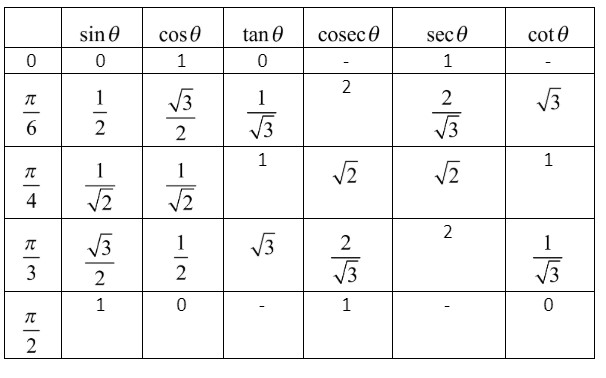
From the above table, we can see that \[\sin \dfrac{\pi }{4}=\dfrac{1}{\sqrt{2}}\]. So by substituting the value of \[\sin \dfrac{\pi }{4}\] in equation (i), we get
\[\sec y=2.\dfrac{1}{\sqrt{2}}\]
\[\sec y=\sqrt{2}\]
From the table we know that
$\cos\dfrac{\pi}{4}=\dfrac{1}{\sqrt{2}}$ and we know that $\cos\theta=\dfrac{1}{\sec\theta}$
We can write \[\sec \dfrac{\pi }{4}=\sqrt{2}\]. So by substituting the value of \[\sqrt{2}\] in terms of sec in the above equation, we get,
\[\sec y=\sec \dfrac{\pi }{4}\]
By taking \[{{\sec }^{-1}}\] on both the sides of the above equation, we get,
\[{{\sec }^{-1}}\left( \sec y \right)={{\sec }^{-1}}\left( \sec \dfrac{\pi }{4} \right)\]
Now we know that the range of principal values of \[se{{c}^{-1}}\] is \[\left[ 0,\pi \right]-\dfrac{\pi }{2}\] and for this value \[{{\sec }^{-1}}\left( \sec 0 \right)=0\]. By applying this in the above equation, we get,
\[y=\dfrac{\pi }{4}\]
Hence, we get the principal value of \[se{{c}^{-1}}\left( 2\sin \left( \dfrac{3\pi }{4} \right) \right)\] as \[\dfrac{\pi }{4}\].

Note: First of all, in these type of questions, students must remember the value of at least \[\sin \theta ,\cos \theta \] and \[\tan \theta \] at general angles like \[{{0}^{o}},{{30}^{o}},{{45}^{o}}\], etc. as values of \[\sec \theta ,\operatorname{cosec}\theta ,\cot \theta \] could be found from these. Students should also verify their answer by substituting the value of y in the initial equation and checking if LHS = RHS. Also, take care whether the answer lies in the range of \[{{\sec }^{-1}}\] or not and if it is a principal solution that is between 0 to \[2\pi \] or not.