Question

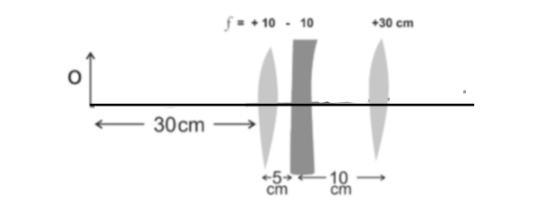
Find the position of the image formed by the lens combination given in the figure.

Answer 1

Hint: The given figure has two lenses and the focal length with the sign is shown in the figure above. One should be aware of the combined lens formula to solve this type of questions and use the concepts of the different types of length.

Complete Step by step solution:
Let us assume that the focal length is denoted by $f$, the object distance is denoted by $u$, and the image distance is $v$ from the lens.
The lens formula to be used in the given question to find the position of the image is as below:
$ \Rightarrow {f_1} = + 10{\text{ cm}}$
$ \Rightarrow {u_1} = \left( { - 30{\text{ cm}}} \right)$
Using the lens formula,
$\dfrac{1}{{{v_1}}} - \dfrac{1}{{{u_1}}} = \dfrac{1}{{{f_1}}}$
On rearranging the above lens formula, we get
$ \Rightarrow \dfrac{1}{{{v_1}}} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{u_1}}}$
By using the value of ${v_1} = 15{\text{ cm}}$
As shown in the figure above, the image of the first lens is formed at the distance of the $15{\text{cm}}$ and this image formed by the first lens will act as the source for the second lens placed at the right of the first lens.
Now, considering the case of the second lens.
${f_2} = - 10{\text{ cm}}$
${u_2} = (15 - 5{\text{) cm}}$
$ \Rightarrow {u_2} = 10{\text{ cm}}$
Again substituting the values in the above given equation we get,
$\dfrac{1}{{{v_2}}} = \dfrac{1}{{{f_2}}} + \dfrac{1}{{{u_2}}}$
$\dfrac{1}{{{v_2}}} = - \dfrac{1}{{10}} + \dfrac{1}{{10}}$
$ \Rightarrow {v_2} = \infty $
The real image thus formed by the second lens at infinite distance. This image will act as an object for the lens that is placed in front of this current image that is for the third lens.
Now calculating the distance of the image that is formed by the third lens is
${f_3} = 30{\text{ cm}}$
${u_3} = \infty $
$\dfrac{1}{{{v_3}}} = \dfrac{1}{{{f_3}}} + \dfrac{1}{{{u_3}}}$
$\dfrac{1}{{{v_3}}} = \dfrac{1}{{30}} + \dfrac{1}{\infty }$
$ \Rightarrow {v_3} = 30{\text{ cm}}$
So, the final position of the image formed on this combination is $30{\text{ cm}}$ to the right of the third lens.

Note:One should know the type of lens used in the combination and the lens formula which is to be applied. Also, one has to have a good knowledge of the direction to be taken as positive and how to proceed.