Question

Find the perimeter of the square with diagonal $ 12\;cm $ ?

Answer 1

Hint: To find the perimeter of a square, first we need the value of any one side of the square. As they have given another clue that they have given the value of the diagonal, by using this value we can find the value of the sides. And don’t forget that all sides of the square are equal.

Complete step-by-step answer:
First of all, the formula for the perimeter of the square is $ 4a $ , where $ a $ is the side of the square. To find the side of the square, let’s solve by using Pythagora's theorem. In that right angled triangle, let consider the diagonal value as the hypotenuse side and other two sides of the triangle are considered the same in case of the square. Applying Pythagoras theorem, we get,

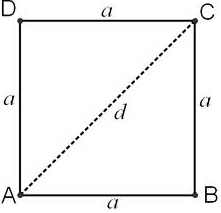
Diagonal $ {d^2} $ = $ {a^2} + {b^2} $
Here in the case of square $ a = b $ and substituting the value of $ d $ in the above equation we get,
 $
  12 = \sqrt {{a^2} + {a^2}} \\
\Rightarrow {12^2} = 2{a^2} \\
\Rightarrow 144 = 2{a^2} \\
\Rightarrow \dfrac{{144}}{2} = {a^2} \\
\Rightarrow {a^2} = 72 \\
\Rightarrow a = 6\sqrt2 \;
  $
The side of the square cannot be in negative value, so we take $ a = 8 $ , substituting the value of $ a $ in the perimeter of the square we get,
Perimeter of the square
 $
   = 4a \\
   = 4\times 6\sqrt2 \\
   = 24 \sqrt2\;
  $
Perimeter of the square $ = 24 \sqrt2 $
This is our required solution.
So, the correct answer is “ $ 24 \sqrt2 $ cm”.

Note: Pythagoras theorem states that, the square of the hypotenuse side is equal to the sum of the square of the other two sides and Pythagoras theorem only applicable to the right-angles triangle. It is one of the most important theorems, which is most frequently used in many mathematical problems.