Question

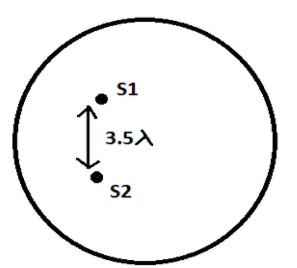
Find the number of maximas obtained on the spherical surface.

Answer 1

Hint: For constructive interference, path difference is \[\text{ }\!\!\Delta\!\!\text{ = n }\!\!\lambda\!\!\text{ }\] and the phase difference is \[\text{ }\!\!\theta\!\!\text{ = 2n }\!\!\pi\!\!\text{ }\] . Using the relation between \[\text{ }\!\!\lambda\!\!\text{ }\] and \[\text{ }\!\!\theta\!\!\text{ }\], calculate order of interference \[\text{(n)}\] and then use it to calculate the number of bright fringes on one part of the screen \[\text{(m)}\]. The total number of fringes will be\[\text{2m}\]
Formulas Used:
\[\text{dsin }\!\!\theta\!\!\text{ = n }\!\!\lambda\!\!\text{ }\]

Complete answer:
In Young’s Double slit experiment, the sources of light used should be coherent sources and of the same frequency.
Two sources are said to be coherent if they are in the same phase or have a constant phase difference.
The waves from both the sources interfere on the screen constructively to give bright fringes and destructively to give dark fringes.
We know that,
\[\text{dsin }\!\!\theta\!\!\text{ = n }\!\!\lambda\!\!\text{ }\]
Where, d = separation between the slits,
\[\text{ }\!\!\theta\!\!\text{ }\] = angle depicting the relative position of the fringe
n = order of interference
\[\text{ }\!\!\lambda\!\!\text{ }\] = wavelength of the light used
Here,
\[\text{ }\!\!\theta\!\!\text{ = 9}{{\text{0}}^{\text{o}}}\] (Because fringes cannot be formed behind the sources)
\[\text{d sin9}{{\text{0}}^{\text{o}}}\text{ = n }\!\!\lambda\!\!\text{ }\]
\[\Rightarrow \text{d = n }\!\!\lambda\!\!\text{ }\] - (1)
According to the question, \[\text{d = 3}\text{.5 }\!\!\lambda\!\!\text{ }\] substituting the value in eq (1), we get,
\[\text{3}\text{.5 }\!\!\lambda\!\!\text{ = n }\!\!\lambda\!\!\text{ }\]
\[\Rightarrow \text{n = 3}\text{.5}\] - (2)
The number of bright fringes (m) is given by,
\[\text{m = 2n-1}\] - (3)
From eq (2) and eq (3), we get,
\[\text{m = 6}\]
Therefore, the number of bright fringes on the upper part of the screen is 6. Similarly, there will be 6 bright fringes on the lower part of the screen too.
So, the total number of fringes is
\[6+6=12\]
Total number of bright fringes formed on the screen is 12.

Note:
In young’s double slit experiment, bright and dark fringes of the same size appear alternatively on the screen. Since, we are using a spherical surface; the brightness of the fringes will decrease towards the center of the screen. Whereas, when we use a straight screen, the brightness of the fringes decrease as we move away from the center of the screen.