Question

Find the number of carbon atoms including the given structure which can have negative change in resonating structure. (The structure with charge repeating are not accepted)

Answer 1

Hint: In organic chemistry, hydrocarbons are an important topic. The hydrocarbons are majorly classified as three groups. There are alkane, alkene and alkyne. The alkane means carbon-carbon single bond. The alkene has a carbon-carbon double bond. The alkyne means carbon-carbon having triple bond in the molecule. In organic chemistry stability of molecules and ions are very important. Carbon ions are classified as two types. There is carbocation and carbanion. The carbon atom which has a positive charge is called carbocation. The carbon atom which has negative charge is called carbocation. In organic chemistry cleavage is split into two types. There are homolytic cleavage and heterolytic cleavage. Ions will happen in heterolytic cleavage. Free radicals will come in Homolytic cleavage.

Complete answer:
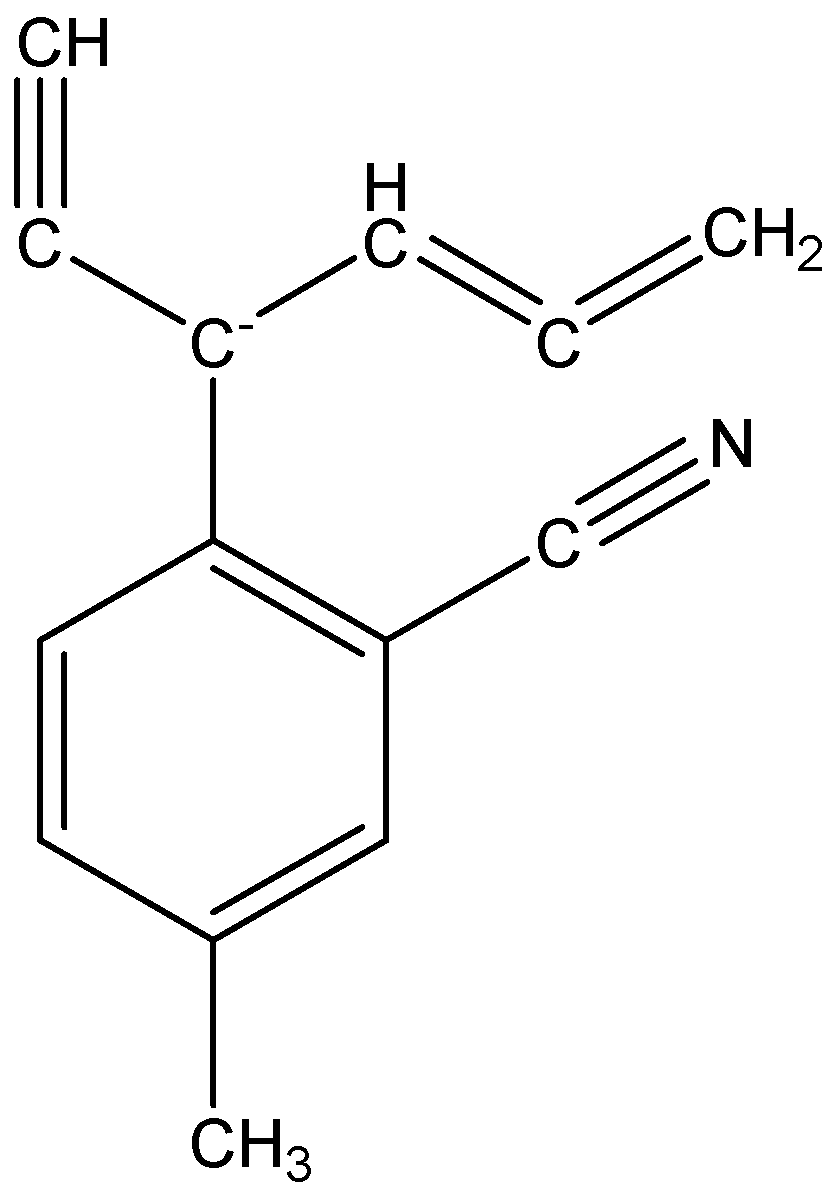
The given structure is

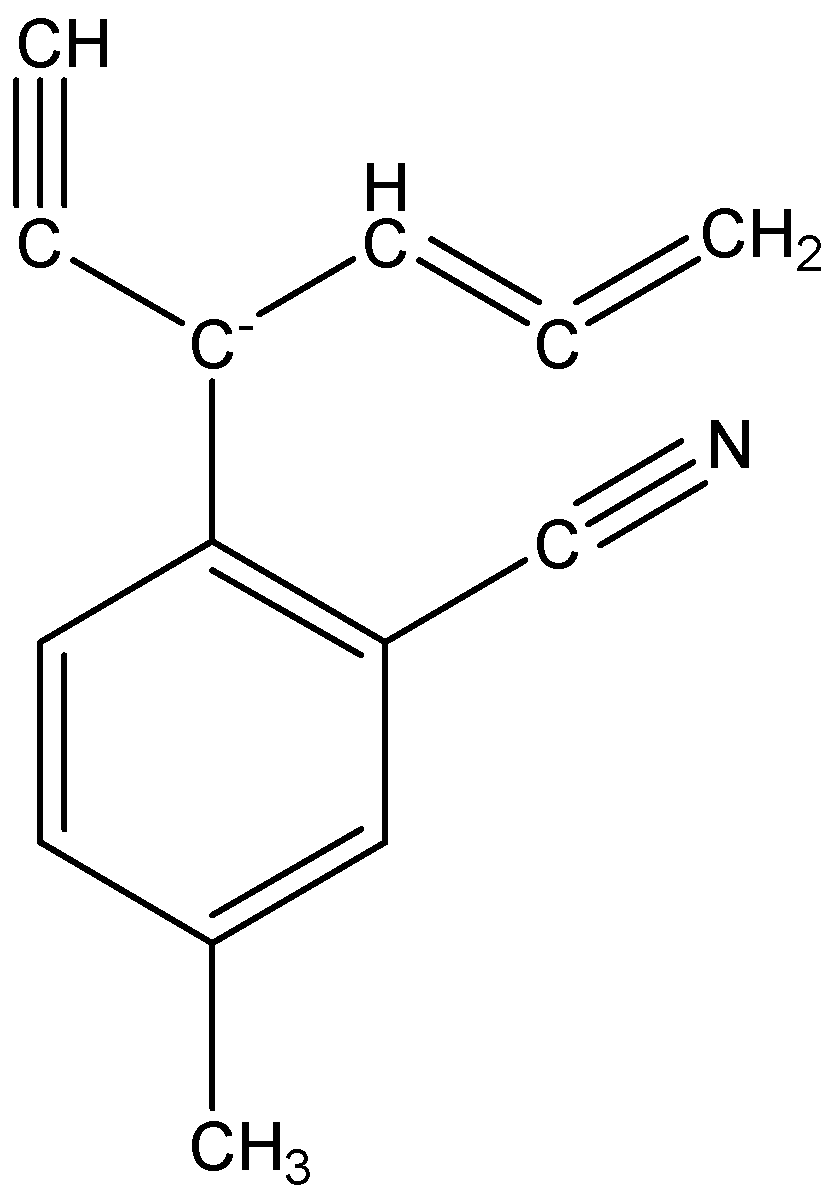
The resonating structure of the given structure which can have negative change in resonating is given below,

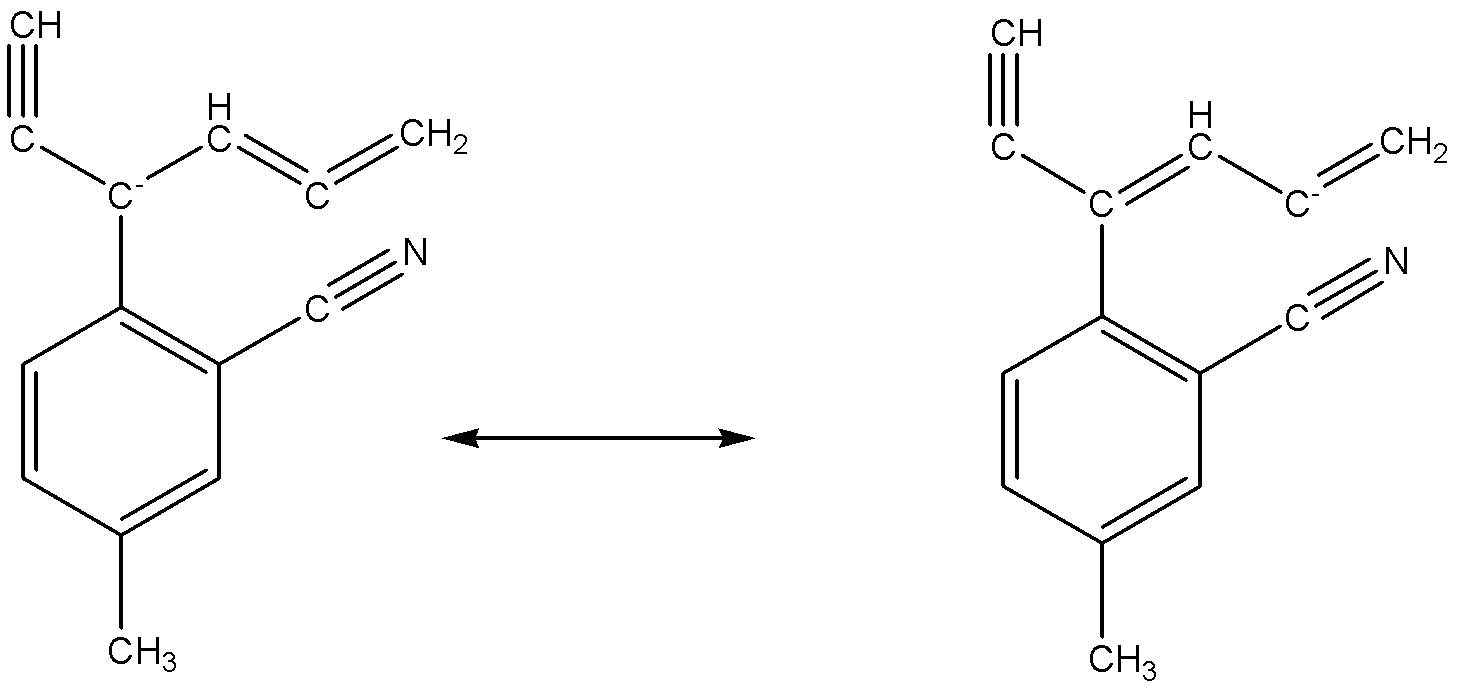
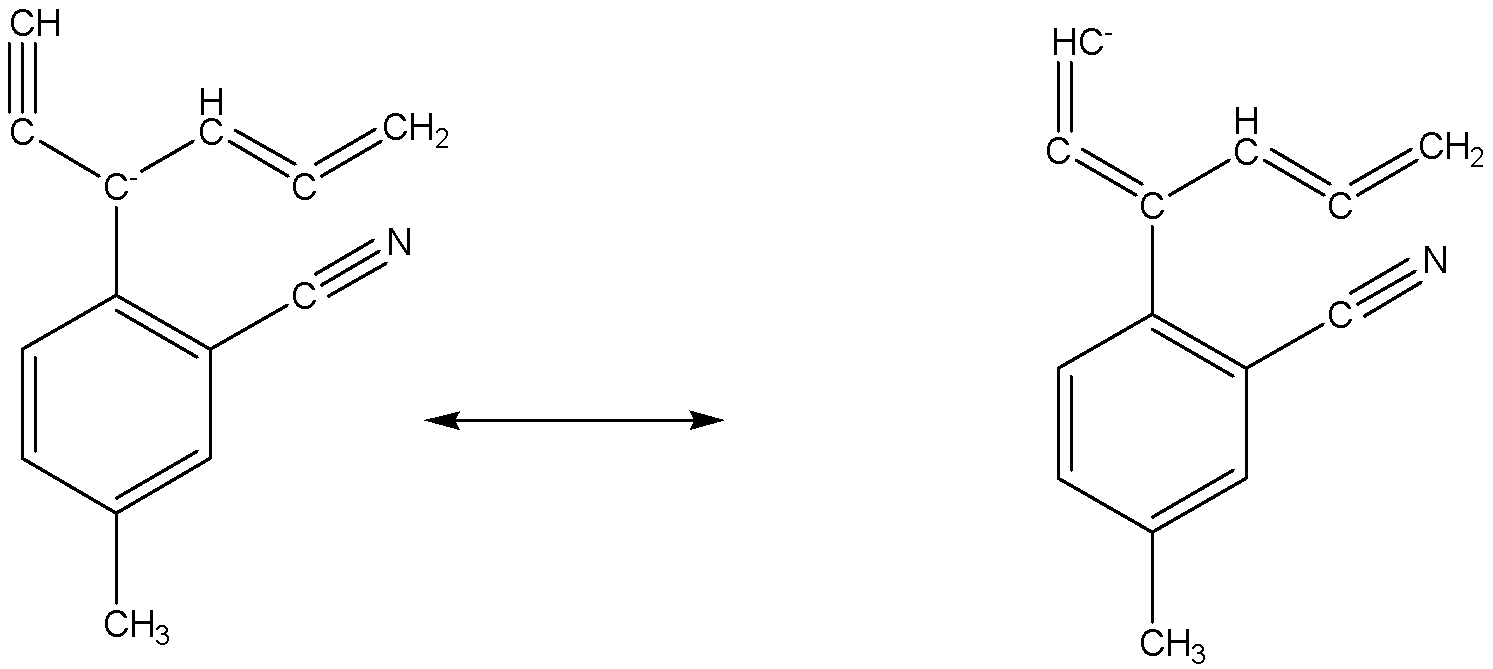
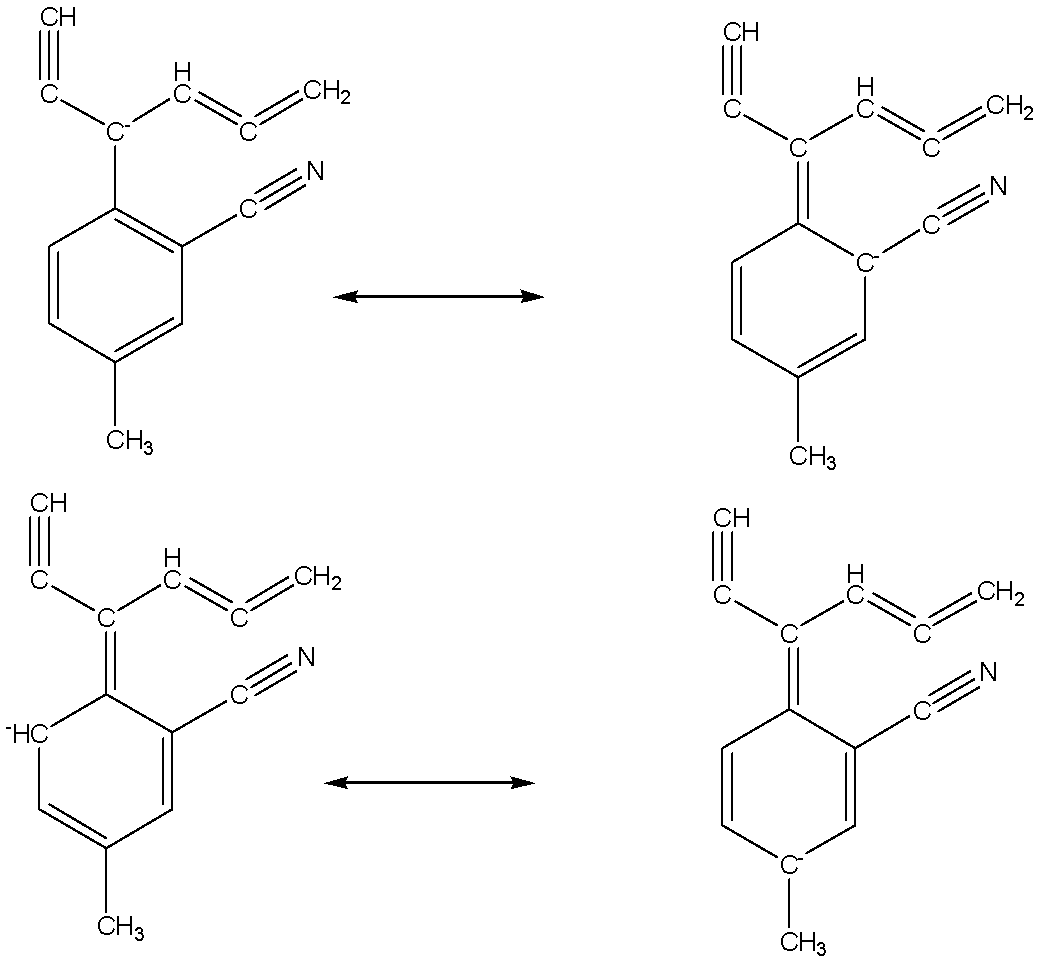
Six number of carbon atoms including the given structure which can have negative change in resonating structures.

Note:
We have to know the conversion of one type of hydrocarbon to another hydrocarbon by oxidation and reduction. The oxidation of alkane to give alkene. The oxidation of alkene to give alkyne. The reduction of alkyne to give alkene. The reduction of alkene to give alkane. It has some general formulas. The general formula of alkane is \[{{\text{C}}_{\text{n}}}{{\text{H}}_{{\text{2n + 2}}}}\]. The general formula of alkene is \[{{\text{C}}_{\text{n}}}{{\text{H}}_{{\text{2n}}}}\]. The general formula of alkyne is \[{{\text{C}}_{\text{n}}}{{\text{H}}_{{\text{2n - 2}}}}\]. The general formula of cycloalkane is \[{{\text{C}}_{\text{n}}}{{\text{H}}_{{\text{2n}}}}\].