
Find the name of the person who first produces a table for solving a triangle’s length and angles.
A. William Rowan Hamilton
B. Hipparchus
C. Euclid
D. Isaac Newton
Answer
573.6k+ views
Hint: He was also an astronomer along with being a mathematician. He is known to have been born in Nicaea in Bithynia. He also introduced the division of a circle into ${360^o}$. He is most famous in the discovery of precession which is due to the slow change in direction of rotation of the earth
Complete step by step solution:
The name of the person who first produced a table for solving a triangle’s length and angles is Hipparchus. He created a table of chords which is equivalent to a table of value of the sine function. The explanation of the construction of the table of chords is given below:
The construction of this table is based on the facts that the chords of ${60^o}\,\,and\,\,{90^o}$ are known, that starting from chord $\theta $ we can calculate chord$({180^o} - \theta )$as shown below:
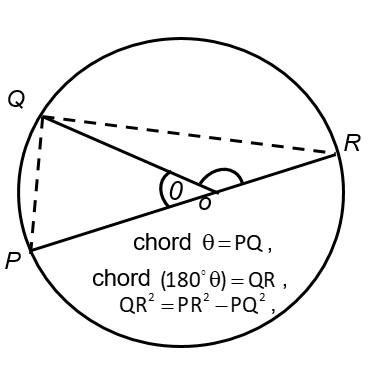
And from the chord $\theta $ we can calculate chord $\dfrac{1}{2}\theta $. The calculation of chord $\dfrac{1}{2}\theta $ goes as follows:
:
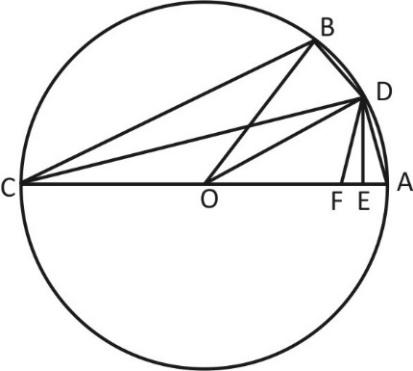
Let the angle $AOB$ be $\theta $. Place $F$ so that $CF = CB$, place $D$ so that $DOA = \dfrac{1}{2}\theta $, and place $E$ so that $DE$ is perpendicular to $AC$. Then $ACD = \dfrac{1}{2}AOD = \dfrac{1}{2}BOD = DCB$making the triangles $BCD\,\,and\,\,DCF$ congruent. Therefore$DF = BD = DA\,\,and\,\,so\,\,EA = \dfrac{1}{2}AF$. But$CF = CB = chord({180^O} - \theta )$, so we can calculate $CF$, which gives us $AF\,\,and\,EA$. Triangles $AED\,\,and\,\,ADC$are similar; therefore $\dfrac{{AD}}{{AE}} = \dfrac{{AC}}{{DA}}$,which implies that $A{D^2} = AE.AC$ and enables us to calculate $AD.AD$is chord $\dfrac{1}{2}\theta $.
We can now find the chords of ${30^o},{15^o},7{\dfrac{1}{2}^o},{45^o}\,\,and\,\,22{\dfrac{1}{2}^o}$.This gives us chord of \[{150^o},{165^o},etc.\]and eventually we have the chords of all.
Multiples of $7{\dfrac{1}{2}^o}$.
We find the chords of angle not listed and angles whole chords are not listed by linear interpolation. For example, the angle whose chord is $2,852$ is $45 + {\left( {\dfrac{{2,852 - 2,631}}{{3,041 - 2,631}} \times 7\dfrac{1}{2}} \right)^o} = {49^o}$ approximately.
Note: Sir William Rowan Hamilton was an Irish mathematician.
Euclid was a Greek mathematician commonly called “founder of Geometry” or “father of Geometry”.
Sir Isaac Newton was an English mathematician. He formulated laws of motion and universal gravitation.
Complete step by step solution:
The name of the person who first produced a table for solving a triangle’s length and angles is Hipparchus. He created a table of chords which is equivalent to a table of value of the sine function. The explanation of the construction of the table of chords is given below:
The construction of this table is based on the facts that the chords of ${60^o}\,\,and\,\,{90^o}$ are known, that starting from chord $\theta $ we can calculate chord$({180^o} - \theta )$as shown below:

And from the chord $\theta $ we can calculate chord $\dfrac{1}{2}\theta $. The calculation of chord $\dfrac{1}{2}\theta $ goes as follows:
:

Let the angle $AOB$ be $\theta $. Place $F$ so that $CF = CB$, place $D$ so that $DOA = \dfrac{1}{2}\theta $, and place $E$ so that $DE$ is perpendicular to $AC$. Then $ACD = \dfrac{1}{2}AOD = \dfrac{1}{2}BOD = DCB$making the triangles $BCD\,\,and\,\,DCF$ congruent. Therefore$DF = BD = DA\,\,and\,\,so\,\,EA = \dfrac{1}{2}AF$. But$CF = CB = chord({180^O} - \theta )$, so we can calculate $CF$, which gives us $AF\,\,and\,EA$. Triangles $AED\,\,and\,\,ADC$are similar; therefore $\dfrac{{AD}}{{AE}} = \dfrac{{AC}}{{DA}}$,which implies that $A{D^2} = AE.AC$ and enables us to calculate $AD.AD$is chord $\dfrac{1}{2}\theta $.
We can now find the chords of ${30^o},{15^o},7{\dfrac{1}{2}^o},{45^o}\,\,and\,\,22{\dfrac{1}{2}^o}$.This gives us chord of \[{150^o},{165^o},etc.\]and eventually we have the chords of all.
Multiples of $7{\dfrac{1}{2}^o}$.
| $\theta $ | \[{0^o}\] | $7{\dfrac{1}{2}^o}$ | ${15^o}$ | $22{\dfrac{1}{2}^o}$ | \[{30^o}\] | \[37{\dfrac{1}{2}^o}\] | ${45^o}$ | $52{\dfrac{1}{2}^o}$ |
| chord$\theta $ | $0$ | $450$ | $897$ | $1,341$ | $1,779$ | $2,210$ | $2,631$ | $3,041$ |
We find the chords of angle not listed and angles whole chords are not listed by linear interpolation. For example, the angle whose chord is $2,852$ is $45 + {\left( {\dfrac{{2,852 - 2,631}}{{3,041 - 2,631}} \times 7\dfrac{1}{2}} \right)^o} = {49^o}$ approximately.
Note: Sir William Rowan Hamilton was an Irish mathematician.
Euclid was a Greek mathematician commonly called “founder of Geometry” or “father of Geometry”.
Sir Isaac Newton was an English mathematician. He formulated laws of motion and universal gravitation.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the Full Form of ISI and RAW




