Question

Find the moment of inertia of a solid cylinder about a transverse (perpendicular) axis passing through its centre.

Answer 1

- Hint: Instead of dealing with the whole cylinder right away, an easier approach would be to divide the cylinder into infinitesimally thin disks. Then, using the moment of inertia of the disk along the central axis, extrapolate it to the transverse axis by using the perpendicular axis theorem and parallel axis theorem. Once you get the resulting moment of inertia for the disk along the transverse axis, integrate it over the entire length of the cylinder to finally arrive at the moment of inertia of the cylinder about its transverse axis.

Formula Used:
Moment of inertia of a disk about its central axis : $I_{disk} = \dfrac{1}{2}mR^2 $, where m is the mass of the disk and R is the radius of the circular part of the disk.
Moment of inertia of a body using Parallel axis theorem: $I = I_c +Mh^2$, where $I_c$ is the moment of inertia of the body about its centre, M is the mass of the body and h is the distance between the two axes.
Moment of inertia of a body using Perpendicular axis theorem: $I = I_1 +I_2$, where $I_1$ and $I_2$ are the moment of inertia of the body in the plane to which the $I$ that we have to find is perpendicular.

Complete step-by-step solution:
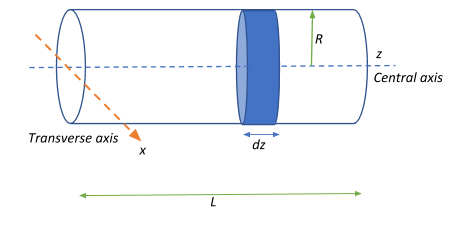
We are required to determine the moment of inertia of a solid cylinder whose axis of rotation is about the transverse x-axis (orange line) that is perpendicular to the cylinder’s central axis.
We can start simple by first cutting the cylinder into infinitesimally thin disks.
Let the length of the cylinder be L and mass of the cylinder be M and radius of the cylinder be R.
Let the volume of the cylinder be $V = \pi R^2L$
Let the thickness (length) of the disk be $dz$. And let the mass of the disk be $dm$.
Volume of the disk $V_{disc} = \pi R^2 dz$

Now, we know that the moment of inertia of a disk about its central axis (z- direction) is:
$I_z = \dfrac{1}{2}mR^2 \Rightarrow dI_z = \dfrac{1}{2}dmR^2$
We know that mass = density $\times$ volume.
Since the density remains uniform throughout the cylinder $\rho = \dfrac{M}{V}$
$\Rightarrow dm = \rho \times V_{disk} = \dfrac{M}{\pi R^2 L} \times (\pi R^2 dz) \Rightarrow dm = \dfrac{M}{L}dz $
Earlier, we have taken the moment of inertia of the disk along the z-axis when we require its moment of inertia along the y-axis which is perpendicular to z. Knowing that the desired axis of rotation is transverse, we can apply the perpendicular axis theorem.
It states that the moment of inertia about an axis, which is perpendicular to the plane containing the remaining two axes, is the sum of the moments of inertia about these two perpendicular axes, passing through the same point of the object.
This follows that $dI_z = dI_x +dI_y$.
Also, owing to symmetry the moment of inertia about the x-axis must be the same as that of the y-axis, i.e.,
$dI_x = dI_y$
$\Rightarrow dI_z = 2dI_x \Rightarrow dI_x = \dfrac{dI_z}{2} = \dfrac{\dfrac{1}{2}dmR^2}{2} = \dfrac{1}{4}dmR^2$
Now, assuming that the disk is located at a distance $z$ from the origin which coincides with the centre of mass we bring in the parallel axis theorem about the x-axis which suggests that the moment of inertia about any axis parallel to the axis through which the centre of mass passes is given by
$I_{parallel\;axis} = I_{CoM} + Mass\times d^2 \Rightarrow dI_x = \dfrac{1}{4}dmR^2 +dmz^2$
We calculated above that $dm = \dfrac{M}{L}dz$ which we substitute in the above equation:
$ dI_x = \dfrac{1}{4}\dfrac{Mdz}{L}R^2 +z^2 \dfrac{Mdz}{L}$
We now integrate the above expression over the length of the entire cylinder.
$I_x = \int_{-\dfrac{L}{2}}^{+\dfrac{L}{2}} dI_x = \int_{-\dfrac{L}{2}}^{+\dfrac{L}{2}} \dfrac{1}{4}\dfrac{M}{L}R^2\;dz + \int_{-\dfrac{L}{2}}^{+\dfrac{L}{2}} z^2 \dfrac{M}{L}dz $
$\Rightarrow I_x = \left[ \dfrac{M}{L}R^2z +\dfrac{M}{L}\dfrac{z^3}{3}\right]_{-\dfrac{L}{2}}^{+\dfrac{L}{2}}$
$\Rightarrow I_x = \dfrac{1}{4}\dfrac{M}{L}R^2 \left[ \dfrac{L}{2} - \left(-\dfrac{L}{2}\right)\right] + \dfrac{M}{3L}\left[\left(\dfrac{L}{2}\right)^3 - \left(-\dfrac{L}{2}\right)^3\right]$
$\Rightarrow I_x = \dfrac{1}{4}\dfrac{M}{L}R^2L + \dfrac{M}{3L}\dfrac{2L^3}{2^3} $
$\Rightarrow I_x = \dfrac{1}{4} MR^2 + \dfrac{1}{12}ML^2 $
Therefore, the moment of inertia of a solid cylinder about a transverse (perpendicular) axis passing through its centre.

Note: Do not get confused between the parallel axis and the perpendicular axis theorems. We use the parallel axis theorem when we want to find the moment of inertia of a body about the axis that is parallel to the axis of the known moment of inertia of the body and passes through the centre of gravity of the object. We use the perpendicular axis theorem when we want to find the moment of inertia of a body about the axis that is perpendicular to the axis of the known moment of inertia of the body and passes through the centre of gravity of the object.