Question

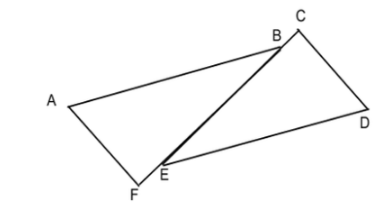
Find the mistake in the proof below.
In \[\Delta ABF\] and \[\Delta CED\]
 \[\overline{AB}\parallel \overline{ED}\] (Given)
 \[\overline{AF}\parallel \overline{CD}\] (Given)
 \[\angle ABF\cong \angle CED\] (Alternate interior angles are congruent as \[\overline{AB}\parallel \overline{ED}\] )
 \[\overline{FE}\cong \overline{BC}\] (Given)
 \[\angle AFB\cong \angle ECD\] (Alternate interior angles are congruent as \[\overline{AF}\parallel \overline{CD}\] )
 \[\therefore \Delta ABF\cong \Delta CED\] (AAS congruency theorem)

Answer 1

Hint: In the given question, we have been asked to find the mistake in the proof of \[\Delta ABF\cong \Delta CED\] . In the given proof, we can observe that the side FE and BC are not the full sides of the given triangle, so we first need to prove that the side FE and BC are equal and therefore the side FB and CE of the two given triangles respectively are equal.

Complete step-by-step answer:
We have given that,
The line segment \[\overline{AB}\] is parallel to the line segment \[\overline{ED}\] .
The line segment \[\overline{AF}\] is parallel to the line segment \[\overline{CD}\] .
Now,
 \[\overline{FE}=\overline{BC~}\]
As,
FE and BC are not the full sides in either of the given triangles.
Using the addition property of equality;
Thus, you will need to add segment BE.
 \[\overline{FE}\cong \overline{BC}\]
Adding the line segment BE to both the sides, we will get
 \[\overline{FE}+\overline{BE}=\overline{BC}+\overline{BE}\]
As \[\overline{BE}\] is common in both the triangles.
Therefore,
 \[\overline{FE}=\overline{BC~}\]
And hence,
 \[\overline{FB}=\overline{CE~}\]
Now,
We have,
 \[\angle ABF\cong \angle CED\] (Alternate interior angles are congruent as \[\overline{AB}\parallel \overline{ED}\] )
 \[\overline{FB}=\overline{CE~}\] (Proof above)
 \[\angle AFB\cong \angle ECD\] (Alternate interior angles are congruent as \[\overline{AF}\parallel \overline{CD}\] )
Thus,
 \[\therefore \Delta ABF\cong \Delta CED\] (ASA congruency theorem)
So, the only mistake in the above proof is that the line segment FE and BC are not the full sides in either of the given triangles.
There is an error in the side needed to prove two triangles congruent by AAS congruence Theorem.

Note: In this type of question, you should know the meaning of congruent triangles and the rules of congruence of two triangles. Different rules of congruence are:
SSS – All sides of one triangle are equal to the corresponding sides of the other triangle.
RHS – In the right triangle, one side and hypotenuse are equal.
ASA – Two angles and the side between both the angles of the two triangles are equal.
SAS – Two sides and one angle between the two sides are equal.