Question

How do you find the missing length for the right triangle below the short side is $9$cm and the hypotenuse is $30$cm?

Answer 1

Hint: We know that in a triangle irrespective of the type of the triangle, the triangle consists of $3$ sides. In a right-angle triangle, we have $3$ sides as Hypotenuse which is opposite to the right angle, Long Side which is bigger in the length of the remaining two, Shorter side is the remaining side in the triangle. In right angle triangle we have the relation between them as $\text{Hypotenus}{{\text{e}}^{2}}=\text{long sid}{{\text{e}}^{2}}+\text{short sid}{{\text{e}}^{2}}$ which is also known as Pythagoras theorem. From the above relation we will substitute the value that are given and we will calculate the required value.

Complete step by step answer:
Given that,
In a right-angle triangle hypotenuse is $30$cm, short side is $9$cm.
Let us assume the third side as $x$cm. Now the typical triangle is shown in figure.

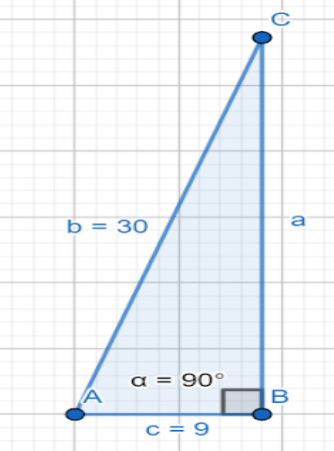
In the above figure the hypotenuse is denoted by $b$ and it is equal to $30$cm, the shorter side is denoted by $c$ and it is equal to $9$cm, Larger side is denoted by $a$.
Applying the Pythagoras theorem in the above triangle, then we will get
${{b}^{2}}={{a}^{2}}+{{c}^{2}}$
Substituting the values, we have in the above equation, then we will get
$\begin{align}
  & \Rightarrow {{\left( 30 \right)}^{2}}={{a}^{2}}+{{9}^{2}} \\
 & \Rightarrow 900={{a}^{2}}+81 \\
 & \Rightarrow {{a}^{2}}=900-81 \\
 & \Rightarrow {{a}^{2}}=819 \\
\end{align}$
Applying the square root on both sides of the above equation, then we will have
$\begin{align}
  & \Rightarrow a=\sqrt{819} \\
 & \therefore a=26.618cm \\
\end{align}$

So, the value of the larger or longer side in the triangle is $26.618$cm.

Note: We can use the above theorem to calculate the value of any side of a right-angle triangle when the remaining two sides are given. But when we have only one side and one angle, then we will use the concept of trigonometry and use the proper trigonometric ratios to calculate the required result.