Question

Find the middle point of the chord intercepted on the line $lx + my + n = 0$ by the circle ${x^2} + {y^2} = {a^2}$.

Answer 1

Hint: Assume the coordinates of the midpoint as some variables $\left( {h,k} \right)$. This point is lying on the chord, so it will satisfy the line equation $lx + my + n = 0$. Frame an equation using this. Further, the line joining the center of the circle with the midpoint of the chord will be perpendicular to the chord. Another equation will be formed using this. Solve both the equations to get the answer.

Complete step-by-step answer:
According to the question, the circle ${x^2} + {y^2} = {a^2}$ intercepts a line $lx + my + n = 0$. We have to determine the midpoint of the chord formed.
Let the line be represented as $L$. So we have:
$ \Rightarrow L:lx + my + n = 0$
We know that the center of the circle ${x^2} + {y^2} = {a^2}$ is at origin with $a$ as its radius. Let the circle is cutting the line $L$ at two different points $A$ and $B$. Then $AB$ is the mentioned chord and let $M$ is the midpoint of this chord as shown in the below figure:
 

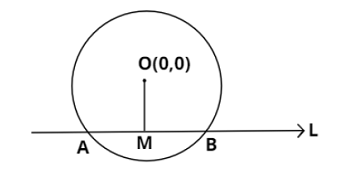
We basically have to determine the coordinates of point $M$. Suppose $\left( {h,k} \right)$ are its coordinates.
Now, since this point $M\left( {h,k} \right)$ lies on the line $L$, the points will satisfy the equation of this line. From this, we’ll get:
$ \Rightarrow lh + mk + n = 0{\text{ }}.....{\text{(1)}}$
Further, $OM$ is the line joining the midpoint of the chord with the center of the circle. This line must be perpendicular to the chord (according to the property of the circle). Thus $OM$ is perpendicular to $L$.
If ${m_1}$ is the slope of $OM$ ($O\left( {0,0} \right),{\text{ }}M\left( {h,k} \right)$), then we have:
$ \Rightarrow {m_1} = \dfrac{{k - 0}}{{h - 0}} = \dfrac{k}{h}{\text{ }}.....{\text{(2)}}$
And if ${m_2}$ is the slope of $L$, then we will rearrange the terms in the equation of $L$ to determine its slope:
$
   \Rightarrow lx + my + n = 0 \\
   \Rightarrow my = - lx - n \\
   \Rightarrow y = - \dfrac{l}{m}x - \dfrac{n}{m} \\
 $
Comparing this with $y = mx + c$, we get the slope of $L$ i.e. ${m_2}$:
$ \Rightarrow {m_2} = - \dfrac{l}{m}{\text{ }}.....{\text{(3)}}$
Since the lines are perpendicular as discussed above and we know that the product of slopes of perpendicular lines is -1, we have:
$ \Rightarrow {m_1} \times {m_2} = - 1$
Putting values from equation (2) and (3), we’ll get:
$
   \Rightarrow \dfrac{k}{h} \times \left( { - \dfrac{l}{m}} \right) = - 1 \\
   \Rightarrow k = \dfrac{{mh}}{l}{\text{ }}.....{\text{(4)}} \\
 $
Putting this value in equation (1), we’ll get:
$
   \Rightarrow lh + m\left( {\dfrac{{mh}}{l}} \right) + n = 0 \\
   \Rightarrow h\left( {l + \dfrac{{{m^2}}}{l}} \right) = - n \\
   \Rightarrow h\left( {\dfrac{{{l^2} + {m^2}}}{l}} \right) = - n \\
 $
On cross multiplication, this will give us:
$ \Rightarrow h = \dfrac{{ - nl}}{{{l^2} + {m^2}}}$
Putting this value in equation (4), we’ll get:
$
   \Rightarrow k = \dfrac{m}{l}\left( {\dfrac{{ - nl}}{{{l^2} + {m^2}}}} \right) \\
   \Rightarrow k = \dfrac{{ - mn}}{{{l^2} + {m^2}}} \\
 $

Thus the coordinates of midpoint of chord i.e. $M$ are $\left( {\dfrac{{ - nl}}{{{l^2} + {m^2}}},\dfrac{{ - mn}}{{{l^2} + {m^2}}}} \right)$

Note: 1. If the perpendicular distance of a line from the center of a circle is less than its radius, then only the line cuts the circle at two different points and a chord is formed.
2. If the perpendicular distance of a line from the center of a circle is equal to its radius then the line only touches the circle at one point and it is a tangent to the circle.
3. And if this perpendicular distance is more than the radius of the circle, then the line does not cut or touch the circle at any point.