Question

How do you find the length of sides of an equilateral triangle inscribed in a circle with a radius of 36?

Answer 1

Hint: We are given that an equilateral triangle is inscribed in a circle of radius and we have to find the measure of each side of the equilateral triangle. A triangle is a two-dimensional shape containing three sides, it is of various types, and a triangle whose all sides are equal is called an equilateral triangle. So, in this question, we can find the measure of all the sides of the triangle by finding out the measure of any one side.

Complete step-by-step answer:

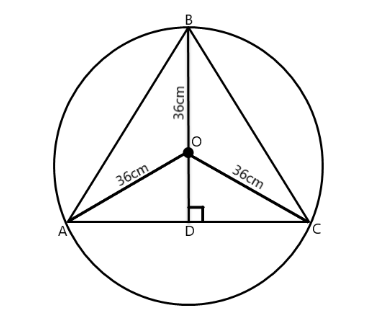
In the figure above, ABC is an equilateral triangle inscribed in a circle of radius 36, BD is perpendicular from the vertex A on the side BC and divides it exactly into two halves, we see that ODC is a right-angled triangle.
We see that $ \angle OCB = \angle OCA = \dfrac{{60^\circ }}{2} = 30^\circ $
We get –
 $
  \cos OCA = \dfrac{{CD}}{{OC}} \\
  \cos 30^\circ = \dfrac{{CD}}{{36}} \\
   \Rightarrow CD = \dfrac{{\sqrt 3 }}{2} \times 36 \;
  $
Now, we know that
 $
  AC = 2CD = 2 \times \dfrac{{\sqrt 3 }}{2} \times 36 \\
   \Rightarrow AC = 36\sqrt 3 \;
  $
Hence, the length of sides of an equilateral triangle inscribed in a circle with a radius of 36 is equal to $ 36\sqrt 3 $ .
So, the correct answer is “ $ 36\sqrt 3 $ ”.

Note: The three sides and the three angles of an equilateral triangle are equal to each other, we know that the sum of the three angles of a triangle is 180 degrees, so each angle of an equilateral triangle is 60 degrees. We can prove $ \angle OCB = \angle OCA = \dfrac{{60^\circ }}{2} = 30^\circ $ by proving that the triangles OCB and OCA are similar to each other. Now, we know the length of one side of the triangles and one of its angles, so we use trigonometric ratios to find the length of the required side.