Question

Find the least number which is divided by 5, 6, 8, 9, 12 leaves a remainder 1 but when divided by 13 leaves no remainder.
A.3601
B.1469
C.2091
D.4879

Answer 1

Hint: Here, we will first find the LCM of 5, 6, 8, 9 and 12. We will assume that the required number is 1 greater than a multiple of the LCM. Then we will find the required number using Euclid’s Division Lemma.

Formulas used:
 We will use the formula of Euclid’s Division lemma which is given by \[a = bq + r\].

Complete step-by-step answer:
Let the required number be \[x\]. We know that when \[x\] is divided by 13, it does not leave any remainder. This means that \[x\] is divisible by 13.
Any number that leaves a remainder of 1 on being divided by 5, 6, 8, 9 and 12 will also leave a remainder of 1 on being divided by the LCM of 5, 6, 8, 9 and 12. We will find the L.C.M. of 5, 6, 8, 9 and 12:

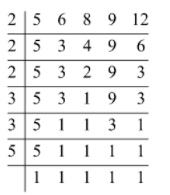
Now, the L.C.M. is given by:
\[\begin{array}{l}{\rm{LCM}} = 2 \times 2 \times 2 \times 3 \times 3 \times 5\\{\rm{LCM}} = 360\end{array}\]
As the number will leave a remainder 1 on being divided by 360, we will substitute 1 for \[r\], \[x\] for \[a\] and 360 for \[b\] in Euclid’s division lemma, \[a = bq + r\]. Therefore, we get
\[x = 360q + 1\]……………………\[\left( 1 \right)\]
We will substitute different values for \[q\] in the above equation and check whether the \[x\] we obtain is divisible by 13. We will do this till we find a number divisible by 13. This method is called the method of trial and error.
Substituting 1 for \[q\] in equation \[\left( 1 \right)\], we get
\[\begin{array}{l}x = 360 + 1\\ \Rightarrow x = 361\end{array}\]
361 is not divisible by 13.
Substituting 2 for \[q\] in equation \[\left( 1 \right)\], we get
\[\begin{array}{l}x = 360\left( 2 \right) + 1\\ \Rightarrow x = 721\end{array}\]
721 is not divisible by 13.
Substituting 3 for \[q\] in equation \[\left( 1 \right)\], we get
\[\begin{array}{l}x = 360\left( 3 \right) + 1\\ \Rightarrow x = 1081\end{array}\]
1081 is not divisible by 13.
Substituting 4 for \[q\] in equation \[\left( 1 \right)\], we get
\[\begin{array}{l}x = 360\left( 4 \right) + 1\\ \Rightarrow x = 1441\end{array}\]
1441 is not divisible by 13.
Substituting 5 for \[q\] in equation \[\left( 1 \right)\], we get
\[\begin{array}{l}x = 360\left( 5 \right) + 1\\ \Rightarrow x = 1801\end{array}\]
1801 is not divisible by 13.
Substituting 6 for \[q\] in equation \[\left( 1 \right)\], we get
\[\begin{array}{l}x = 360\left( 6 \right) + 1\\ \Rightarrow x = 2161\end{array}\]
2161 is not divisible by 13.
Substituting 7 for \[q\] in equation \[\left( 1 \right)\], we get
\[\begin{array}{l}x = 360\left( 7 \right) + 1\\ \Rightarrow x = 2521\end{array}\]
2521 is not divisible by 13.
Substituting 8 for \[q\] in equation \[\left( 1 \right)\], we get
\[\begin{array}{l}x = 360\left( 8 \right) + 1\\ \Rightarrow x = 2881\end{array}\]
2881 is not divisible by 13.
Substituting 9 for \[q\] in equation \[\left( 1 \right)\], we get
\[\begin{array}{l}x = 360\left( 9 \right) + 1\\ \Rightarrow x = 3241\end{array}\]
3241 is not divisible by 13.
Substituting 10 for \[q\] in equation \[\left( 1 \right)\], we get
\[\begin{array}{l}x = 360\left( {10} \right) + 1\\ \Rightarrow x = 3601\end{array}\]
3601 is divisible by 13.
$\therefore $ The least number which is divided by 5, 6, 8, 9, 12 leaves a remainder 1 but when divided by 13 leaves no remainder is 3601.
Option A is the correct option.

Note: The above method is a lengthy and tedious method. We can also find the answer by choosing the least number from the options and checking whether it is divisible by 13 and leaves a remainder of 1 on being divided by 360. Option B is divisible by 13 but doesn’t leave a remainder of 1 on being divided by 360. Option C is not divisible by 13. Option fulfils both the criteria, so it’s the correct option.
If a number (say \[a\]) on being divided by another number (say b) leaves a remainder \[r\] and has a divisor \[q\], then according to Euclid’s Division lemma: \[a = bq + r\]
where \[0 \le r < b\] and \[a\] and \[b\] are integers.