Question

Find the largest number that divides 2053 and 967 and leaves a remainder of 5 and 7 respectively.

Answer 1

Hint: H.C.F can be defined as the highest number which divides the given numbers and gives remainder zero. Apply this rule to get an answer.

Let us suppose that number is ‘N’ which divides 2053 and 967 and leaves a remainder 5 and 7 respectively.
Now, the first number is given as 2053 which is divided by N and given remainder 5. Now, if we subtract 5 from 2053, we get 2053 – 5 = 2048 which will give remainder zero if we divide it by N now.
For second number 967, if we divide it by N, we get remainder 7 which means if we divide 967 – 7 =960 by N, we will get remainder zero.
Hence, now one can rewrite the question as evaluating the number which divides 2048 and 960 and gives remainder 0.
Now, we can relate that number N should be the highest common factor of 2048 and 960 which will divide the given numbers and the remainder will be zero.
So, let us find H.C.F by prime factorization method.
Prime factorization of 960 can be given as;

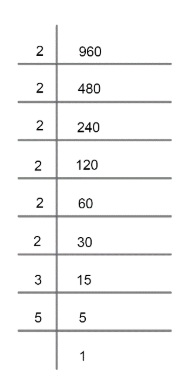
Hence,
$960=2\times 2\times 2\times 2\times 2\times 2\times 3\times 5$ …………………..(1)
Now, factoring 2048 as

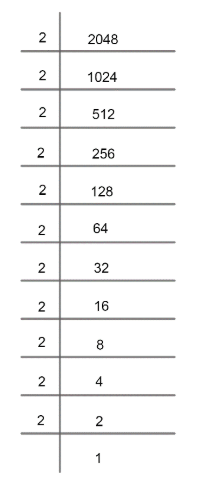
Hence, 2048can be expressed as;
$2048=2\times 2\times 2\times 2\times 2\times 2\times 2\times 2\times 2\times 2\times 2$ ………………..(2)
Now, as we know the prime factorization method that the terms common in the factorization of numbers will give the HCF.
Hence, common factors in 960 and 2048;
\[H.C.F=2\times 2\times 2\times 2\times 2\times 2={{2}^{6}}\]
H.C.F = 64
Hence, number N is 64 which will give remainders 5 and 7 on dividing 2053 and 967 respectively.

Note: One can go wrong after subtraction of remainders from the given numbers. He/she may go for calculation of L.C.M (Least common multiple) in place of H.C.F which will give the wrong solution.
Hence, terms H.C.F and L.C.M should be very clear for this question.
One can miss any prime factor from the expression of prime factorization of 960 and 2048.