Question

How do you find the intercepts of \[y = 2{x^2} - 5x + 2\] ?

Answer 1

Hint: Here in this question, we have to plot the graph for the equation. By substituting the x is equal to zero we can find the y intercept value and substituting y is equal to zero we can find the x intercept value. By equating the given equation to the general equation of line we can determine the slope. Here we have found the x intercepts.

Complete step by step solution:
An intercept is a point where the straight line or a curve intersects the y-axis in a plane. If the point x is zero then the obtained point is a y -intercept.
Now consider the given equation \[y = 2{x^2} - 5x + 2\] -----------(1)
Substitute the value of y as 0 in the equation (1) then we have
\[ \Rightarrow 0 = 2{x^2} - 5x + 2\]
To determine the value of x we use the formula \[x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\]. Here the value of a is 2 and the value of b is -5 and the value of c is 2
Hence by substituting these values in the formula we get
\[ \Rightarrow x = \dfrac{{ - ( - 5) \pm \sqrt {{{( - 5)}^2} - 4(2)(2)} }}{{2(2)}}\]
On simplifying we get
\[ \Rightarrow x = \dfrac{{5 \pm \sqrt {25 - 16} }}{4}\]
On subtracting 16 from 25 we get
\[ \Rightarrow x = \dfrac{{5 \pm \sqrt 9 }}{4}\]
The square root of 9 is 3
\[ \Rightarrow x = \dfrac{{5 \pm 3}}{4}\]
Therefore, we have \[x = \dfrac{{5 + 3}}{4}\] and \[x = \dfrac{{5 - 3}}{4}\]
On simplifying we get
\[x = \dfrac{8}{4} = 2\] and \[x = \dfrac{{5 - 3}}{4} = \dfrac{1}{2}\]
Therefore, x-intercept are \[\left( {2,0} \right)\] and \[\left( {\dfrac{1}{2},0} \right)\]
We can also find the y- intercept
Substitute the value of x as 0 in equation (1), then we have
\[ \Rightarrow y = 2{(0)^2} - 5(0) + 2\]
On simplifying we get
\[ \Rightarrow y = 2\]
Therefore, y-intercept is \[\left( {0,2} \right)\]
Hence we have found the x intercepts and also the y intercepts.
The graph for this is given below

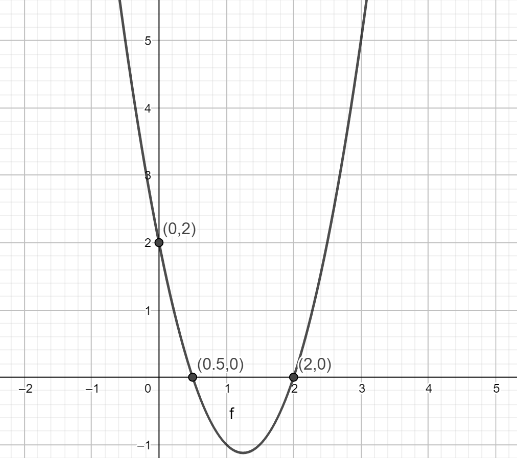
Note: The question is belonging to the concept of graph. By comparing the given equation to the equation of a line we calculate the slope and intercept. Or by choosing the value of x we can determine the value of y and then plotting the graphs for these points we obtain the result.