Question

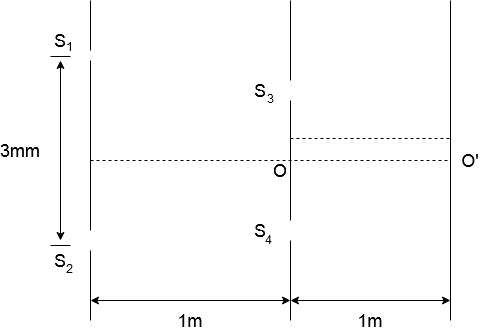
Find the intensity at $O'$(on the screen)
A.$4.5{I_0}$
B.$3{I_0}$
C.$2{I_0}$
D.$5{I_0}$

Answer 1

Hint: You can start by describing what interference is. Calculate the intensity at ${S_3}$ by using the equation ${S_3} = {(\sqrt {{I_0}} + \sqrt {{I_0}} )^2}$ and calculate the value of $\cos \delta $ by using the equation ${S_4} = {I_0} + {I_0} + 2{I_0}\cos \delta $. Then calculate the intensity at \[O'\] by using the equation \[O' = 4{I_0} + {I_0} + 2(\sqrt {{I_0}} )(2\sqrt {{I_0}} )\cos \delta \].

Complete answer:
In physics interference is a very important phenomenon. Interference involves the superimposition of two waves which forms a resultant with amplitude more, less or the same as the two waves involved. There are also two specific conditions that are important for us – constructive and destructive interference. For constructive and destructive interference it is very important that the two waves either come from the same source or have the same or nearly the same frequency. Interference occurs in all types of waves including but not limited to acoustic, surface water waves, gravity waves, matter water and light waves.
In interference the amplitude of the resultant wave, is a vector sum of the amplitude of the two waves. If a crest of one wave meets a crest of another wave, then the amplitude is the sum of amplitude of the two waves. If a crest of one wave meets the trough of another waves then the amplitude of the resultant wave is the difference in the amplitude of the two waves.
Intensity at ${S_3}$ will be equal to the maximum intensity that can be obtained on the first screen due to ${S_1}$ and ${S_2}$
Intensity at ${S_3} = {(\sqrt {{I_0}} + \sqrt {{I_0}} )^2}$
$ = {(2\sqrt {{I_0}} )^2}$
$ = 4{I_0}$
Intensity at ${S_4} = {I_0} + {I_0} + 2{I_0}\cos \delta $
${I_0} = {I_0} + {I_0} + 2{I_0}\cos \delta $
$\cos \delta = - \dfrac{1}{2}$
Here we can see that there is phase difference between the rays meeting at ${S_4}$.
Given in the image associated with the problem is that the point $O'$ is equidistant from both point ${S_4}$ and ${S_3}$. Since the rays meet at the same time, the phase difference will be equal to $\delta $.
The intensity at point \[O' = 4{I_0} + {I_0} + 2(\sqrt {{I_0}} )(2\sqrt {{I_0}} )\cos \delta \]
The intensity at point \[O' = 5{I_0} - 2{I_0}\]
The intensity at point \[O' = 3{I_0}\]
Hence, option B is the correct choice.

Note: As discussed earlier to produce constructive and destructive interference, we need two waves from the same source or with constant phase difference. In labs, white light is not usually used to demonstrate interference, normally we use sodium lamps as a single light source for the two waves.