Question

Find the inductance of a unit length of two parallel wires, each of radius \[a\], whose centers are at distance \[d\] apart and carry equal currents in opposite directions. Neglect the flux within the wire.
(A) \[\dfrac{{\mathop \mu \nolimits_0 }}{{2\pi }}\ln \left( {\dfrac{{d - a}}{a}} \right)\]
(B) \[\dfrac{{\mathop \mu \nolimits_0 }}{\pi }\ln \left( {\dfrac{{d - a}}{a}} \right)\]
(C) \[\dfrac{{\mathop {3\mu }\nolimits_0 }}{\pi }\ln \left( {\dfrac{{d - a}}{a}} \right)\]
(D) \[3\dfrac{{\mathop \mu \nolimits_0 }}{\pi }\ln \left( {\dfrac{{d - a}}{a}} \right)\]

Answer 1

Hint: As we know that the magnetic field due to an infinite long straight wire carrying current \[I\], has the same magnitude at all points that are at the same distance from the wire. i.e., the magnetic field has cylindrical symmetry around the wire and given by the formula-
\[B = \dfrac{{\mathop \mu \nolimits_0 }}{{4\pi }}\dfrac{{2I}}{r}\] ………………………. (1)
Where \[\mathop \mu \nolimits_0 = \]absolute magnetic permeability of free space, \[I = \]current carried out by conducting wires, and \[r = \]distance of points from wire where the magnetic field is to be calculated.
And, the magnetic flux through any surface can be calculated by given equation-
\[\mathop \phi \nolimits_B = \int_i^f {\overrightarrow B } \cdot \overrightarrow {ds} \] ………………... (2)
Where \[\overrightarrow B = \]Magnetic field, \[\overrightarrow {ds} = \]small area element, and \[i\], \[f\] are initial and final limits through which integral will be carried out.

Complete step by step solution:
Step 1: In this given problem two wires of infinite length and both are having radius \[a\] are taken into account. Each wire is carrying current \[I\] in the same direction.

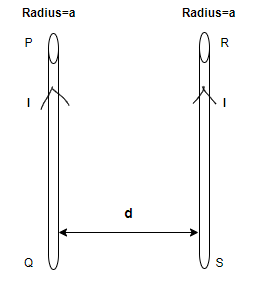
The given wires are of infinite length so the whole system can be considered as a closed rectangle PQRS of infinite length and breadth equal to the distance between the two conducting wires i.e., \[d\].
So, the flux associated within this closed system will be equal to the flux associated with wire PQ (let it be \[\mathop \phi \nolimits_1 \] ) because of wire RS plus the flux associated with wire RS (let it be \[\mathop \phi \nolimits_2 \] ) because of wire PQ.
So, \[\mathop \phi \nolimits_1 = \mathop \phi \nolimits_2 = \int_a^{d - a} {\dfrac{{\mathop \mu \nolimits_0 }}{{4\pi }}} \dfrac{{2I}}{r}\left( {ldr} \right)\] where \[ldr = \]small area element
\[\mathop \phi \nolimits_1 = \mathop \phi \nolimits_2 = \int_a^{d - a} {\dfrac{{\mathop \mu \nolimits_0 }}{{2\pi }}} lI\dfrac{{dr}}{r}\]
\[\mathop \phi \nolimits_1 = \mathop \phi \nolimits_2 = \dfrac{{\mathop \mu \nolimits_0 }}{{2\pi }}lI\left[ {\ln r} \right]_a^{d - a}\]
\[\mathop \phi \nolimits_1 = \mathop \phi \nolimits_2 = \dfrac{{\mathop \mu \nolimits_0 }}{{2\pi }}lI\ln \left( {\dfrac{{d - a}}{a}} \right)\] ……………... (3)
Step 2: The total flux through the rectangle PQRS is given by \[\mathop \phi \nolimits_t = \mathop \phi \nolimits_1 + \mathop \phi \nolimits_2 \] ……………... (4)
By substituting the values of \[\mathop \phi \nolimits_1 \] and \[\mathop \phi \nolimits_2 \] from equation (3), we will get-
 \[\mathop \phi \nolimits_t = 2\mathop \phi \nolimits_1 \]
\[\mathop \phi \nolimits_t = 2\dfrac{{\mathop \mu \nolimits_0 }}{{2\pi }}lI\ln \left( {\dfrac{{d - a}}{a}} \right)\]; after putting the value from equation (3)
\[\mathop \phi \nolimits_t = \dfrac{{\mathop \mu \nolimits_0 }}{\pi }lI\ln \left( {\dfrac{{d - a}}{a}} \right)\] …………….. (5)
Step 3: We know that total inductance is given by-
\[L = \dfrac{{\mathop \phi \nolimits_t }}{I}\] ………………... (6)
Where \[\mathop \phi \nolimits_t = \]total flux, and \[I = \]strength of current flowing in the conductor
From equation (5) and (6), we will get-
\[L = \dfrac{{\dfrac{{\mathop \mu \nolimits_0 }}{\pi }lI\ln \left( {\dfrac{{d - a}}{a}} \right)}}{I}\]
\[L = \dfrac{{\mathop \mu \nolimits_0 }}{\pi }l\ln \left( {\dfrac{{d - a}}{a}} \right)\] ……………... (7)
Step 4: So, inductance per unit length is will be given by
\[\dfrac{L}{l} = \dfrac{{\dfrac{{\mathop \mu \nolimits_0 }}{\pi }l\ln \left( {\dfrac{{d - a}}{a}} \right)}}{l}\]; on rearranging the equations
\[\dfrac{L}{l} = \dfrac{{\mathop \mu \nolimits_0 }}{\pi }\ln \left( {\dfrac{{d - a}}{a}} \right)\]

So, the final correct option is (B).

Note:
- Using ampere’s law magnetic field can be calculated for current conducting wires.
- It should be noted while integrating the magnetic field times a small area element if the initial and final points are the same i.e. surface is closed surface the flux associated with the system will be zero.