Question

Find the HCF and LCM of 144, 180 and 192 by prime factorization method.

Answer 1

Hint: Before attempting this question one should have prior knowledge about the HCF and LCM also remember to factorize the number and then take common prime factors and their smallest exponents for HCF and greatest exponents for LCM.

Complete step-by-step answer:
We have to find LCM and HCF using prime factorization method
Factor tree of 144 will be

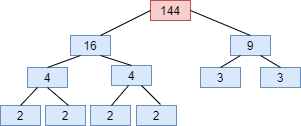
Factor tree of 180 will be

Factor tree of 192 will be

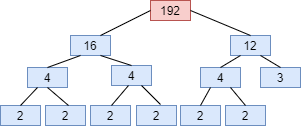
Using factor tree for the prime factorization of 144, 180 and 192 we have
$ \Rightarrow 144 = {2^4} \times {3^2}$
$ \Rightarrow 180 = {2^2} \times {3^2} \times 5$
$ \Rightarrow 192 = {2^6} \times 3$
To find HCF we list the common prime factor and their smallest exponents in 144, 180 and 192 as follows
HCF $ = {2^2} \times {3^1} = 12$
To find LCM we list the common prime factor and their greatest exponents in 144, 180 and 192 as follows
LCM $ = {2^6} \times {3^2} \times {5^1} = 64 \times 9 \times 5 = 2880$

Note: For finding LCM and HCF we have to first factorize the number and making factor tree eg: $144 = {2^4} \times {3^2}$ and then take common prime factors and their smallest exponents for HCF and list all prime factors and their greatest exponents for LCM.