Question

Find the foot of the perpendicular from the point (0, 2, 3) on the line $\dfrac{{x + 3}}{5} = \dfrac{{y - 1}}{2} = \dfrac{{z + 4}}{3}$. Also, find the length of the perpendicular.

Answer 1

Hint: In this particular question use the concept that in the equation of line $\dfrac{{x - {x_1}}}{p} = \dfrac{{y - {y_1}}}{q} = \dfrac{{z - {z_1}}}{r}$, $\left( {{x_1},{y_1},{z_1}} \right)$ are the points of either point joining the line, and (p, q, r) are the direction ratios of the line later on in the solution use the concept that the multiplication of direction ratios of the given line and the foot of the perpendicular is always zero as these lines are perpendicular to each other, so use these concepts to reach the solution of the question.

Complete step-by-step solution:

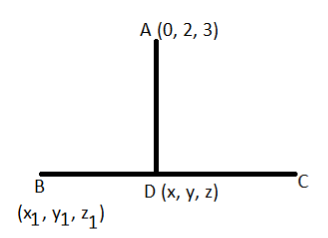
Now as we know that the equation of the line joining two points say B and C is given as,
$ \Rightarrow \dfrac{{x - {x_1}}}{p} = \dfrac{{y - {y_1}}}{q} = \dfrac{{z - {z_1}}}{r}$
Where, $\left( {{x_1},{y_1},{z_1}} \right)$ are the points of either point B or point C.
And (p, q, r) is the direction ratios.
So consider the points of B therefore,
The equation of the line joining points B and C is given which is,
$\dfrac{{x + 3}}{5} = \dfrac{{y - 1}}{2} = \dfrac{{z + 4}}{3}$
So the point, $\left( {{x_1},{y_1},{z_1}} \right)$ = (-3, 1, -4) and the direction ratios is, (p, q, r) = (5, 2, 3)
Now let the foot of the perpendicular from the point A (0, 2, 3) on the line BC be D (x, y, z), as shown in the above figure.
Where (x, y, z) is the variable times the direction cosines of line BC and the sum of the point B.
Let the variable be m, where m is any real number.
Therefore, x = 5m – 3, y = 2m + 1 and z = 3m – 4.
Now let the direction ratios of the line passing from point A and the foot of perpendicular on the line BC be (t, u, v).
So, (t, u, v) = points of A – points of D
So, t = (0 – 5m + 3), u = (2 – (2m + 1)) and v = (3 – (3m – 4))
Therefore, t = -5m + 3, u = 1 – 2m, v = 7 – 3m.
Now the product of direction ratios of line BC and the direction ratios of the foot of the perpendicular line is always zero so we have,
$ \Rightarrow pt + qu + rv = 0$
Now substitute the values we have,
 $ \Rightarrow 5\left( { - 5m + 3} \right) + 2\left( {1 - 2m} \right) + 3\left( {7 - 3m} \right) = 0$
Now simplify this we have,
$ \Rightarrow - 25m + 15 + 2 - 4m + 21 - 9m = 0$
$ \Rightarrow - 38m + 38 = 0$
$ \Rightarrow m = \dfrac{{ - 38}}{{ - 38}} = 1$
So the point D (x, y, z) is
$x = 5m – 3, y = 2m + 1 \text{ and } z = 3m – 4.$
Therefore, $x = 5 – 3, y = 2 + 1 \text{ and } z = 3 – 4$.
Therefore, $D = (x, y, z) = (2, 3, -1)$
Now we have to find out the length of this foot of the perpendicular.
So as we know that the distance between two points $\left( {{x_1},{y_1},{z_1}} \right){\text{ and }}\left( {{x_2},{y_2},{z_2}} \right)$ is given as,
$ \Rightarrow d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}} $
Now let, point A = $\left( {{x_1},{y_1},{z_1}} \right)$ = (0, 2, 3)
And point D = $\left( {{x_2},{y_2},{z_2}} \right)$ = (2, 3, -1)
So the perpendicular distance is
$ \Rightarrow d = \sqrt {{{\left( {2 - 0} \right)}^2} + {{\left( {3 - 2} \right)}^2} + {{\left( { - 1 - 3} \right)}^2}} $
$ \Rightarrow d = \sqrt {4 + 1 + 16} $
$ \Rightarrow d = \sqrt {21} = 4.58$ Units.
So this is the required answer.

Note: Whenever we face such types of questions the key concept we have to remember is that the coordinates of the foot of the perpendicular in line BC are the variable (say m) times the direction cosines of line BC and the sum of the point B, so first find out the direction cosines of line BC then find out the coordinates of the foot of perpendicular on line BC then find out the direction cosines of this perpendicular line then multiplication of the direction cosines is always zero so from this calculate the value of m and hence calculate the point D (i.e. foot of the perpendicular) as above then apply the distance formula between two points as above we will get the required length of the perpendicular.