Question

How do you find the focus of a parabola $x={{y}^{2}}+4$ ?

Answer 1

Hint: In this question we have been asked to find the focus of a parabola $x={{y}^{2}}+4$ . From the basic concepts we know that for any expression of a parabola in the form of $x=a{{y}^{2}}+by+c$ the vertex $P$ is $\left( h,k \right)$ where $k=\dfrac{-b}{2a}$ and $h$ is the value of $x$ for $y=k$ in the given expression. The focus $S$ of a parabola is located at a distance of $\dfrac{1}{4a}=SP$ .

Complete step by step solution:
Now considering from the question we have to find the focus of a parabola $x={{y}^{2}}+4$ .
From the basic concepts we know that for any expression of a parabola in the form of $x=a{{y}^{2}}+by+c$ the vertex $P$ is $\left( h,k \right)$ where $k=\dfrac{-b}{2a}$ and $h$ is the value of $x$ for $y=k$ in the given expression. The focus $S$ of a parabola is located at a distance of $\dfrac{1}{4a}=SP$ .
Now we will first find the vertex and then evaluate for the focus.
The vertex will be $P\left( h,k \right)$ where $k=\dfrac{-b}{2a}=0$ and $\Rightarrow h={{0}^{2}}+4\Rightarrow h=4$ .
Hence the vertex $P$ of parabola is $\left( 0,4 \right)$ . Now we need to evaluate the focus of the parabola.
We know the distance between focus $S$ and vertex $P$ is given as $SP=\dfrac{1}{4a}\Rightarrow \dfrac{1}{4}$ .
Therefore the focus will be $\left( 4.25,0 \right)$.

Note:
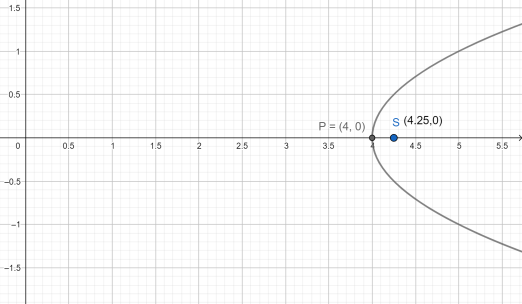
While answering this question our concept should be clear and the calculations we apply should be accurate. While solving we may get tricked and confused in between if we don’t visualise the graph of the given parabola in mind even sometimes we can draw it on the rough paper. While finding the distance someone may think of using the distance formula $\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$ . But here it becomes a very complex method if we can visualise the graph then it becomes simple as the whole graph lies in the first and fourth quadrants. The graph of the parabola looks like the one below: