Question

Find the equivalent resistance from A to B in the network shown in the figure.

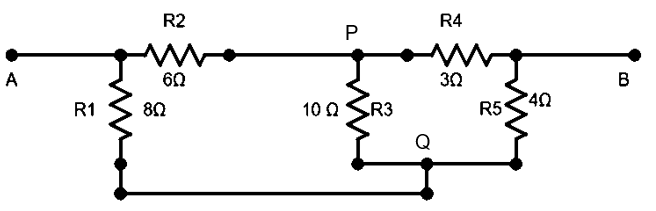
Answer 1

Hint: We are to find the equivalent resistance of the series-parallel combination of the network between the points A and B. We can analyse the circuit after knowing whether the resistances are connected in series or parallel to each other.

Complete step by step answer:
We are given a series-parallel combination of resistors between the points A and B. We can calculate the equivalent circuit by considering each of the circuit elements and their positions with respect to each other.

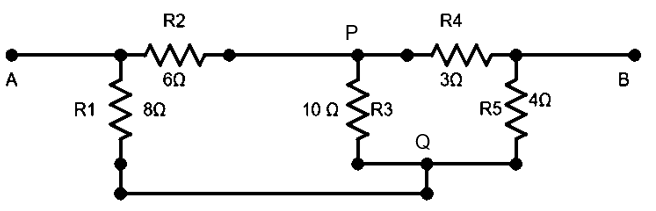
From the figure of the circuit, we can understand that the points P and Q are at the same potential by the Wheatstone’s condition. The condition is satisfied as –
\[\begin{align}
  & \dfrac{R1}{R5}=\dfrac{R2}{R4} \\
 & \Rightarrow \dfrac{8\Omega }{4\Omega }=\dfrac{6\Omega }{3\Omega }=\dfrac{1}{2} \\
\end{align}\]
The points P and Q are equipotential and therefore, no current passes through the resistor R3. Now, we can consider a simplified circuit without the resistor R3 as –
   

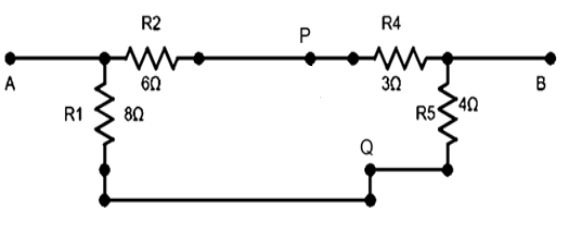
We can understand very easily that the resistors R1, R5 and R2, R4 are parallel pairs, which are in series to each other.
So, we can calculate the resistance of the set of series resistors as –
\[\begin{align}
  & {{R}_{s1}}=R1+R5 \\
 & \Rightarrow {{R}_{s1}}=12\Omega \\
\end{align}\]
The second set of series pairs give the resistance as –
\[\begin{align}
  & {{R}_{s2}}=R4+R2 \\
 & \Rightarrow {{R}_{s2}}=9\Omega \\
\end{align}\]
Now, we can calculate the equivalent resistance as \[{{R}_{s1}}||{{R}_{s2}}\]. The equivalent resistance of the given network is given by –
\[\begin{align}
  & \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{s1}}}+\dfrac{1}{{{R}_{s2}}} \\
 & {{R}_{eq}}=\dfrac{{{R}_{s1}}{{R}_{s2}}}{{{R}_{s1}}+{{R}_{s2}}} \\
 & \Rightarrow {{R}_{eq}}=\dfrac{12.9}{12+9} \\
 & \therefore {{R}_{eq}}=5.142\Omega \\
\end{align}\]
This gives the resistance of the above circuit.
Therefore, the equivalent resistance of the given circuit is 5.142\[\Omega \].

Note:
The Wheatstone’s bridge condition is one of the most useful conditions in the series-parallel networks in which the computation of equivalent resistance is not easily possible. The Meter bridge and the potentiometer also work on applying this condition.