Question

Find the equation of the line AB in the following figure, given $OP=\dfrac{3}{2}$.\[\]

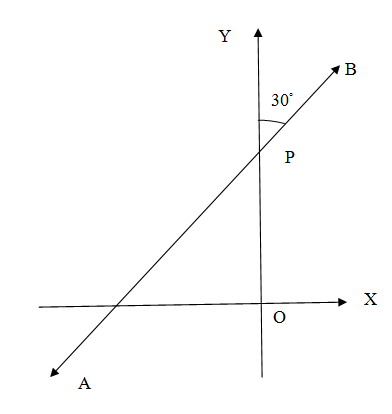
Answer 1

Hint:We find the equation of the line AB in slope point form with slope $m$ and a point on the line $\left( {{x}_{1}},{{y}_{1}} \right)$ as $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$. We find co-ordinate of the point P lying on the line using$OP=\dfrac{3}{2}$. We find the slope of AB taking tangent of the angle AB makes with positive $x-$axis whose measurement we find using the angle ${{30}^{\circ }}$ that AB subtends with $y-$axis in the figure.\[\]

Complete step by step answer:
We see in the given figure that the starlight line AB is inclined on $y-$axis in the coordinate plane. The line AB intersects the $y-$axis at point P and also subtends an angle of ${{30}^{\circ }}$We take a point R above the point P which also lies on the $y-$ axis. We denote the point of intersection of the line AB with the $x-$axis as Q and the angle of inclination the line AB makes with the positive direction of $x-$axis as $\theta .$ We have the constructed figure as,\[\]

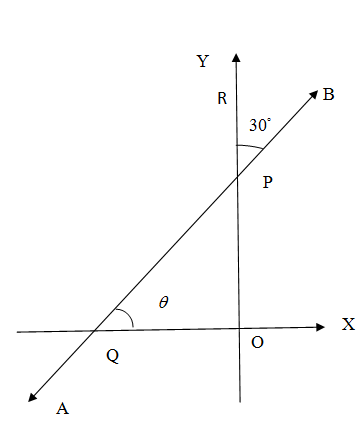
We know the $x-$coordinate of any point is the distance of the point M from the $y-$axis and the $y-$coordinate is called ordinate is the distance of the point M from the $x-$axis .Then we can write the co-ordinates of M as$M\left( x,y \right)$. Here the$y-$coordinate of the point is equal to OP which given in the question as $OP=\dfrac{3}{2}$ and the $x-$coordinate is 0 as P lies on $y-$axis. So the coordinate of the P is $P\left( 0,\dfrac{3}{2} \right).$\[\]
We have $\angle RPB=\angle OPQ={{30}^{\circ }}$ because the both angles are vertical opposite to each other. We have the right angle$\angle POQ={{90}^{\circ }}$. We use the property that sum of internal angles in a triangle is ${{180}^{\circ }}$ to find$\angle PQO=\theta $. So we have
\[\begin{align}
  & \angle POQ+\angle PQO+\angle OPQ={{180}^{\circ }} \\
 & \Rightarrow {{90}^{\circ }}+\theta +{{30}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow \theta ={{60}^{\circ }} \\
\end{align}\]
We know that the slope of a line is tangent of the angle it makes with positive $x-$axis in anticlockwise direction. Here the lien AB makes angles $\theta $ with positive $x-$axis. So the slope $m$ of AB is
\[\tan \theta =\tan \left( {{60}^{\circ }} \right)=\sqrt{3}\]
We know the equation of the line in slope point form with slope $m$ and a point on the line $\left( {{x}_{1}},{{y}_{1}} \right)$ as
\[y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)\]
The slope of the line AB is $m=\sqrt{3}$ and the point $P\left( 0,\dfrac{3}{2} \right)$ lies on it. So the equation of the line AB is
\[\begin{align}
  & y-\dfrac{3}{2}=\sqrt{3}\left( x-0 \right) \\
 & \Rightarrow 2y-3=2\sqrt{3}x \\
 & \Rightarrow 2\sqrt{3}x+2y-3=0 \\
\end{align}\]
Note:
We can also find the equation of the any line with slope $m$ and $y-$intercept $c$ is given by $y=mx+c.$ Here in this problem$c=\dfrac{3}{2}$. The equation of the lines with two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ is given by $y-{{y}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right)$.