Question

How do you find the equation for the parabola with the vertex $\left( 1,4 \right)$ that passes through the point $\left( 3,8 \right)$?

Answer 1

Hint: To solve the given question we will use the standard formula of vertex form of parabola $y=a{{\left( x-h \right)}^{2}}+k$ , where $\left( h,k \right)$ are the coordinates of vertex and \[\left( x,y \right)\] are the coordinates of point from which parabola passes through and a is the distance of origin from the focus. Then substituting the values and simplifying the obtained equation we will get the desired answer.

Complete step-by-step solution:
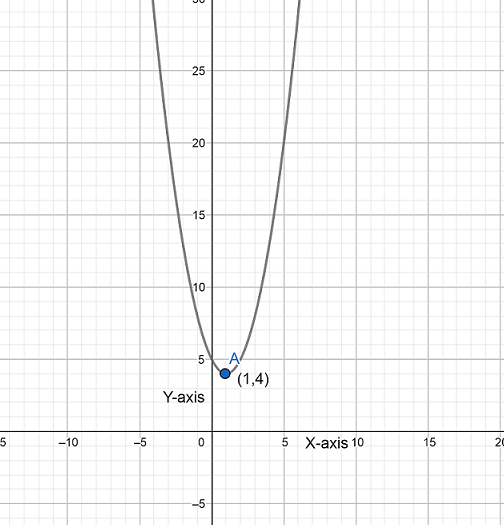
We have given the vertex of parabola $\left( 1,4 \right)$ that passes through the point $\left( 3,8 \right)$.
We have to find the equation of parabola.
Now, we know that the vertex form of equation of parabola is given as $y=a{{\left( x-h \right)}^{2}}+k$ , where $\left( h,k \right)$ are the coordinates of vertex and \[\left( x,y \right)\] are the coordinates of point from which parabola passes through and a is the distance of origin from the focus.
Here we have the coordinates of vertex $\left( h,k \right)$ as $\left( 1,4 \right)$and the coordinates of point from which parabola passes through is $\left( 3,8 \right)$.
Now, substituting the values in the general equation we will get
$\begin{align}
  & \Rightarrow y=a{{\left( x-h \right)}^{2}}+k \\
 & \Rightarrow 8=a{{\left( 3-1 \right)}^{2}}+4 \\
\end{align}$
Now, simplifying the above obtained equation we will get
$\begin{align}
  & \Rightarrow 8=a{{\left( 2 \right)}^{2}}+4 \\
 & \Rightarrow 8-4=4a \\
 & \Rightarrow 4=4a \\
 & \Rightarrow a=1 \\
\end{align}$
Hence the required equation of parabola is $y=1{{\left( x-1 \right)}^{2}}+4$.

Note: Vertex of a parabola is the highest or lowest point of the parabola which is also known as maximum or minimum point. Also it is important to know the basic concepts of parabola to solve such types of questions. Here if the value of a=-ve then the parabola would have the downward facing.