Question

Find the dimensions of the rectangle of the largest area that can be inscribed in a circle of radius r.

Answer 1

Hint: A rectangle has two dimensions namely length and breadth. To find its maximum value, we differentiate the function and put the obtained derivative equal to zero. But for differentiating the area function, we have to first convert it into a function of only one variable. As the radius of the circle is constant, its derivative will be zero so use the relation between length, breadth and radius of the circle to find out the correct answer.

Complete step-by-step answer:

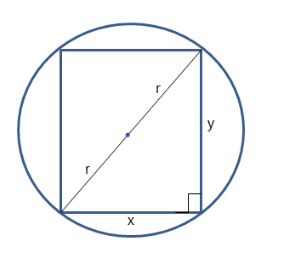
Let a rectangle of dimensions $ x \times y $ be inscribed in a circle of radius r.
Applying Pythagoras theorem on the right-angled triangle,
 $
\Rightarrow {x^2} + {y^2} = {(2r)^2} \\
\Rightarrow {x^2} + {y^2} = 4{r^2} \\
\Rightarrow {y^2} = 4{r^2} - {x^2} \\
\Rightarrow y = \sqrt {4{r^2} - {x^2}} \;
  $
As dimensions of any shape cannot be negative so $ y = - \sqrt {4{r^2} - {x^2}} $ is not considered.
Area of the rectangle,
 $
\Rightarrow A = x \times y \\
\Rightarrow A = x\sqrt {4{r^2} - {x^2}} \;
  $
Differentiating both sides with respect to x, we get –
 $ \dfrac{{dA}}{{dx}} = \dfrac{d}{{dx}}(x\sqrt {4{r^2} - {x^2}} ) $
Use the product rule to differentiate the above result –
 $
  {A^1}(x) = x\dfrac{{d(\sqrt {4{r^2} - {x^2}} )}}{{dx}} + \sqrt {4{r^2} - {x^2}} \dfrac{{d(x)}}{{dx}} \\
  {A^1}(x) = x\dfrac{{d\sqrt {4{r^2} - {x^2}} }}{{d(4{r^2} - {x^2})}}\dfrac{{d(4{r^2} - {x^2})}}{{dx}} + \sqrt {4{r^2} - {x^2}} (1) \\
  {A^1}(x) = x\dfrac{1}{{2\sqrt {4{r^2} - {x^2}} }}( - 2x) + \sqrt {4{r^2} - {x^2}} \\
  {A^1}(x) = \dfrac{{ - {x^2} + 4{r^2} - {x^2}}}{{\sqrt {4{r^2} - {x^2}} }} \\
  {A^1}(x) = \dfrac{{ - 2{x^2} + 4{r^2}}}{{\sqrt {4{r^2} - {x^2}} }} \;
  $
Now to get the maximum value, put $ {A^1}(x) = 0 $
 $
  \dfrac{{ - 2{x^2} + 4{r^2}}}{{\sqrt {4{r^2} - {x^2}} }} = 0 \\
   \Rightarrow 4{r^2} = 2{x^2} \\
  {x^2} = 2{r^2} \\
  x = \sqrt 2 r \;
  $
The negative value of x is rejected.
 $ \Rightarrow y = \sqrt {4{r^2} - {x^2}} = r\sqrt 2 $
 $
  A(r\sqrt 2 ) = r\sqrt 2 (\sqrt {4{r^2} - 2{r^2}} \\
  A(r\sqrt 2 ) = r\sqrt 2 (r\sqrt 2 ) = 2{r^2} \;
  $
The maximum area of a rectangle inscribed in a circle is $ 2{r^2}\,units $ and its dimensions are $ r\sqrt 2 \,units \times r\sqrt 2 \,units $ .
So, the correct answer is “ $ 2{r^2}\,units $ ”.

Note: To verify that the area found out is the maximum, we take the second derivative test.
If the second derivative comes out to be negative at that point then the point gives maximum value and if the second derivative comes out to be positive then the point gives minimum value. You can verify the above answer by doing its second derivative test. We also observe that the length is equal to the breadth of the rectangle for the maximum area that is a rectangle of maximum area that can be inscribed in a circle is a square.