Question

Find the degrees of the angle subtended the centre of a circle by an arc whose length is 15 cm, if the radius of the circle is 25 cm.

Answer 1

Hint: First of all, let us assume a circle whose centre is A and whose radius is equal to 25 cm. Use the fact that if the distance between any two points on the circle is equal to \[l\], angle subtended by these two points is equal to \[\theta \] and r is radius of the circle then \[l=r\theta \]. From this formula, we will find the value of \[\theta \]. We will get the value of \[\theta \] in radians. We know that \[1\text{ radian = }\dfrac{180}{\pi }\text{ degrees}\]. We also know that \[\pi =\dfrac{22}{7}\]. From these formulae, we should convert the angle in radians to degrees.

Complete step-by-step answer:
Let us assume a circle whose centre is A and whose radius is equal to 25 cm. Let us assume two points on the circle B and C where the length of BC is equal to 15 cm.

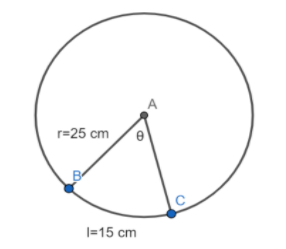
So, let us assume the distance between B and C in the above diagram is equal to \[l\]. Then, we get
\[\Rightarrow l=15.....(1)\]
Let us assume the radius of the circle is equal to r. Then, we get
\[\Rightarrow r=25....(2)\]
Let us assume the angle subtended by the points B and C at the centre A is equal to \[\theta \].
We know that if the distance between any two points on the circle is equal to \[l\], angle subtended by these two points is equal to \[\theta \] and r is radius of the circle then \[l=r\theta \].
So, from equation (1) and equation (2), then we get
\[\Rightarrow 15=25\left( \theta \right)\]
From cross multiplication, then we get
\[\begin{align}
  & \Rightarrow \theta =\dfrac{15}{25} \\
 & \Rightarrow \theta =\dfrac{3}{5} \\
 & \Rightarrow \theta =0.6\text{ radians}....\text{(3)} \\
\end{align}\]
We know that
\[1\text{ radian = }\dfrac{180}{\pi }\text{ degrees}....\text{(4)}\]
Let us substitute equation (4) in equation (3), then we get
\[\begin{align}
  & \Rightarrow \theta =\left( 0.6 \right)\left( \dfrac{180}{\pi } \right)\text{ degrees} \\
 & \Rightarrow \theta =\left( \dfrac{108}{\pi } \right)\text{ degrees} \\
\end{align}\]
We know that \[\pi =\dfrac{22}{7}\].
\[\begin{align}
  & \Rightarrow \theta \text{=34}\text{.36 degrees} \\
 & \Rightarrow \theta =34{}^\circ 36\grave{\ } \\
\end{align}\]
So, we can say that the angle subtended the centre of a circle by an arc whose length is 15 cm, if the radius of the circle is 25 cm is equal to \[34{}^\circ 36\grave{\ }\].

Note: Students may have a misconception that \[1\text{ radian = }\dfrac{\pi }{180}\text{ degrees}\]. This misconception will give us a different value of \[\theta \] in degrees. But the exact value of the angle in degrees is equal to \[34{}^\circ 36\grave{\ }\]. So, this misconception should be avoided to get a correct answer. Students should have clarity in this concept to have an accurate answer.