Question

Find the degree measure of the angle subtended at the center of a circle of radius 100cm by an arc of length 22 cm (Use $\pi =\dfrac{22}{7}$ ).

Answer 1

Hint:Use the formula $l=r\theta $ where s is arc length and r is radius of the given circle and then use it to find $\theta $ which will be in radian. Then multiply with $\dfrac{180}{\pi }$ to get the result.

Complete step-by-step answer:
In the question, we are given a circle of radius 100 cm and an arc length of 22 cm and we have to find angle subtended by arc.

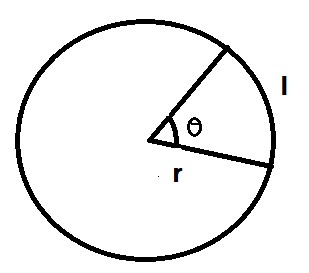
From the figure let consider r be the radius of circle 100cm and l be the arc length of 22cm we have to find $\theta$ .
Before proceeding we will first briefly say something about radian.
The radian is a S.I. unit for measuring angles and is the standard unit of angular measure used in areas of mathematics. The length of an arc of a unit circle is numerically equal to the measurement in radians of the angle that it subtends; one radian is just under 57.3 degrees.
Radian describes the plain angle subtended by a circular arc as the length of arc divided by radius of the arc. One radian is the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle. The magnitude in radius of such a subtend angle is equal to the ratio of the arc length to the radius of circle; that is $\theta =\dfrac{l}{r}$ , where $\theta $ is the subtended angle in radius, l is arc length and r is radius.
Conversely, the length of the enclosed arc is equal to the radius multiplied by the magnitude of the angle in radius that is $l=r\theta $ .
Now to find the angle we will use the formula $l=r\theta $ where l is arc length, r is radius of circle and $\theta $ is angle in radian.
We know l is 22 cm and r is 100 cm.
So, the value of $\theta $ is $\dfrac{l}{r}$ or $\dfrac{22cm}{100cm}$ or 0.22 radian .
Now to convert radius into degrees we have to multiply with $\dfrac{180}{\pi }$ or $\dfrac{180}{\dfrac{22}{7}}$ or $\dfrac{180\times 7}{22}$
So, we get $0.22\times \dfrac{180\times 7}{22}$
The degree subtended by arc is $12.6{}^\circ $ .

Note: Students generally misunderstand the quantity of $\theta $. Generally most students have confusion that ‘ $\theta $ ‘ in the question is in degree or in radian. So, they should clearly know that value of $\theta $ in radian.Students should remember to convert from degree to radian one should multiply by $\dfrac{\pi }{180}$ to get the value in radians and to convert from radian to degree one should multiply by $\dfrac{180 }{\pi}$ to get the value in degrees.