Question

Find the current through the $ 6\Omega $ and $ 4\Omega $ resistances.

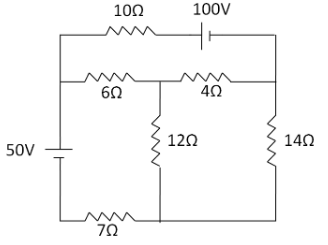
Answer 1

Hint: To solve this question, consider the three meshes given in the circuit and find the currents in each mesh. Then, using the values of mesh currents, find the values of current through the resistances.

Complete step by step solution:
Let us consider the current in the three meshes as $ {I_1} $ , $ {I_2} $ and $ {I_3} $ respectively, as in the given diagram.

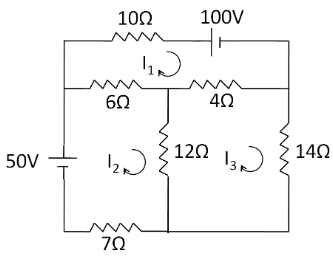
Applying KVL in the mesh containing $ {I_1} $ current, we have
 $ 10{I_1} + 100 + 4({I_1} - {I_3}) + 6({I_1} - {I_2}) = 0 $
 $ 20{I_1} + 100 - 4{I_3} - 6{I_2} = 0 $
On rearranging, we get
 $ - 20{I_1} + 6{I_2} + 4{I_3} = 100 $
Dividing both sides by $ 2 $
 $ - 10{I_1} + 3{I_2} + 2{I_3} = 50 $ …………….(1)
Now, applying KVL in the mesh containing $ {I_2} $
 $ 6({I_2} - {I_1}) + 12({I_2} - {I_3}) + 7{I_2} - 50 = 0 $
 $ - 6{I_1} + 25{I_2} - 12{I_3} = 50 $…………….(2)
Finally, applying KVL in the mesh containing $ {I_3} $
 $ 4({I_3} - {I_1}) + 14{I_3} + 12({I_3} - {I_2}) = 0 $
 $ - 4{I_1} - 12{I_2} + 30{I_3} = 0 $
Dividing both sides by $ - 2 $
 $ 2{I_1} + 6{I_2} - 15{I_3} = 0 $ …………….(3)
Subtracting (1) from (2), we have
 $ - 6{I_1} + 25{I_2} - 12{I_3} - ( - 10{I_1} + 3{I_2} + 2{I_3}) = 50 - 50 $
 $ 4{I_1} + 22{I_2} - 14{I_3} = 0 $
Dividing both sides by $ 2 $
 $ 2{I_1} + 11{I_2} - 7{I_3} = 0 $ …………….(4)
Applying cross-multiplication method in (3) and (4), we have
 $ \dfrac{{{I_1}}}{{123}} = \dfrac{{{I_2}}}{{ - 16}} = \dfrac{{{I_3}}}{{10}} = \lambda $ , where $ \lambda $ is some real number
 $ \therefore {I_1} = 123\lambda ,{\text{ }}{I_2} = - 16\lambda ,{\text{ }}{I_3} = 10\lambda $...............(5)
Substituting these in (1), we get
 $ - 10(123\lambda ) + 3( - 16\lambda ) + 2(10\lambda ) = 50 $
 $ - 1258\lambda = 50 $
So, we get
 $ \lambda = - \dfrac{{50}}{{1258}} $
Putting this in (5)
 $ {I_1} = - \dfrac{{6150}}{{1258}} = - 4.89A $ , $ {I_2} = \dfrac{{800}}{{1258}} = 0.64A $ , and $ {I_3} = - \dfrac{{500}}{{1258}} = - 0.39A $
Now, current through the $ 6\,\Omega $ resistance
 $ {I_{6\Omega }} = {I_2} - {I_1} $
Putting the values, we get
 $ {I_{6\Omega }} = 0.64 - ( - 4.89) $
 $ {I_{6\Omega }} = 5.53A $
Also, the current through the $ 4\Omega $ resistance
 $ {I_{4\Omega }} = {I_3} - {I_1} $
Putting the values
 $ {I_{4\Omega }} = - 0.39 - ( - 4.89) $
 $ {I_{4\Omega }} = 4.5A $
Hence $ {I_{6\Omega }} = 5.53A $ and $ {I_{4\Omega }} = 4.5A $ .

Note:
While using KVL, first select a sign convention and then proceed. Do not get confused due to the sign convention. The choice of sign convention doesn’t change the final answer. We can use any one of the two sign conventions for the resistances and the batteries.