Question

How do you find the coterminal with the angle $-{{45}^{\circ }}$ ?

Answer 1

Hint: We are given angle as $-{{45}^{\circ }}$ , we are asked to find learning what negative in front of angle means, then we learn about coterminal angle, once we get that we work with some example to get the understanding, we learn coterminal angle using graphical representation. Then we work on our problem with angle $-{{45}^{\circ }}$ .

Complete step by step answer:
We are given as $-{{45}^{\circ }}$ , we are asked to find the coterminal angle with the angle $-{{45}^{\circ }}$ .
Firstly we will understand that the negative sign symbolic the orientation.
Now we work on our problem, we start by understanding what are coterminal angles.
coterminal angles are angles in standard position that mean angles with the initial side on the positive x-axis and have the common terminal side.
For example ${{30}^{\circ }}$ and $-{{330}^{\circ }}$ .
If we sketch them on graph, we get better understanding

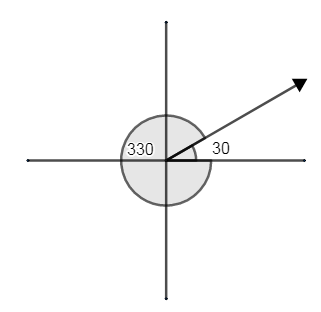
Here ${{30}^{\circ }}$ and $-{{330}^{\circ }}$ start from the positive axis, and have a common terminal.
So, they are coterminal angles by definition.
They can be more than 1 coterminal angle for any given angle, like for 30, apart from -330 degree, we have 390degree.

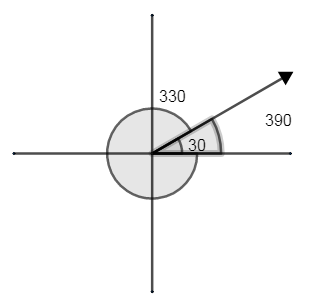
In general, if $\theta $ is any angle whose initial side is positive x-axis then $\theta +n\left( {{360}^{\circ }} \right)$ is coterminal angle with $\theta $ where ‘n’ is non zero integer.
Now, we work on our problem, we have $-{{45}^{\circ }}$ , we are asked to find angle coterminal with $-{{45}^{\circ }}$.
We start by considering $-{{45}^{\circ }}$as $\theta $ , so $\theta =-45$ .
As we know that for angle $\theta $ , coterminal angle is given as $\theta +{{360}^{\circ }}n$
So, for $\theta =-{{45}^{\circ }}$ .
Its coterminal angle is $-{{45}^{\circ }}+n\left( {{360}^{\circ }} \right)$ .
We put $n=1$ , we get –
$\begin{align}
  & -{{45}^{\circ }}+{{360}^{\circ }}\times 1 \\
 & \Rightarrow -{{45}^{\circ }}+{{365}^{\circ }} \\
 & ={{315}^{\circ }} \\
\end{align}$
So, we get a coterminal angle with angle $-{{45}^{\circ }}$is ${{315}^{\circ }}$ .

Note:
Depending upon ‘n’, we can have many other coterminal angle also graphically

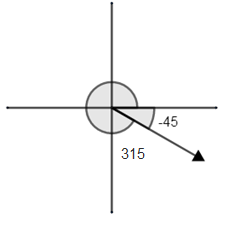
So, for $-{{45}^{\circ }}$ , ${{315}^{\circ }}$ is coterminal.
Remember that positive or negative sign in the angle is regard to the orientation, if we measure angle in clockwise direction this it is negative, if we measure anti-clock wise then it is positive also graph way to find coterminal angle is also strong as we can clearly see whether condition of being coterminal angle are satisfied or not.