Question

Find the circular projection of the vector $\hat{i}+3\hat{j}+7\hat{k}$ on the vector $2\hat{i}-3\hat{j}+6\hat{k}$

Answer 1

Hint: We will first of all use the formula of scalar projection of one vector on another. The projection of a vector $\vec{a}$ on another vector $\vec{b}$ is given by $\dfrac{\vec{a}\cdot \vec{b}}{\left| {\vec{b}} \right|}$
Where, $\vec{a}\cdot \vec{b}$ is the dot product of $\vec{a}\text{ and }\vec{b}$ and $\left| {\vec{b}} \right|$ is the magnitude of vector $\vec{b}$ Then, we will use formula of dot product of two vectors and magnitude of a vector to calculate the end result.
Dot product of two vectors $\vec{p}\text{ and }\vec{q}$ where \[\vec{p}=x\hat{i}+y\hat{j}+z\hat{k}\text{ and }\vec{q}= x'\hat{i}+y'\hat{j}+z'\hat{k}\] given by
\[\vec{p}\cdot \vec{q}=xx'+yy'+zz\text{ }\!\!'\!\!\text{ }\]
Here, we have two vectors given in the question, so we will first find their dot product and then the projection using the above information.
Let us assume both the given vectors as variables.
Let \[\vec{a}=\hat{i}+3\hat{j}+7\hat{k}\text{ and }\vec{b}=2\hat{i}-3\hat{j}+6\hat{k}\]

Complete step-by-step solution:
To solve this question, we will use the formula of the scalar projection of a vector on another vector.
The projection of a vector $\vec{a}$ on another vector $\vec{b}$ is given by $\dfrac{\vec{a}\cdot \vec{b}}{\left| {\vec{b}} \right|}$
Where, $\vec{a}\cdot \vec{b}$ is the dot product of $\vec{a}\text{ and }\vec{b}$ and $\left| {\vec{b}} \right|$ is the magnitude of vector $\vec{b}$
It works like:

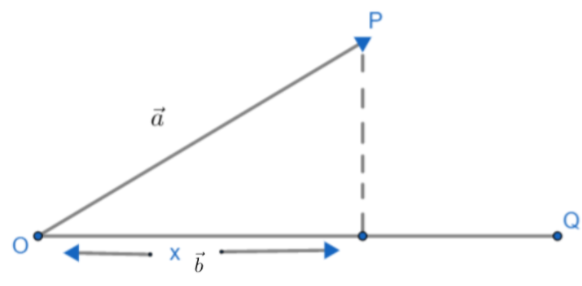
x is projection of \[\vec{a}\text{ on }\vec{b}\]
\[\begin{align}
  & OP=\vec{a} \\
 & OQ=\vec{b} \\
\end{align}\]
Dot product of two vector $\vec{p}\text{ and }\vec{q}$ where \[\vec{p}=x\hat{i}+y\hat{j}+z\hat{k}\text{ and }\vec{q}=x'\hat{i}+y'\hat{j}+z'\hat{k}\] given by
\[\vec{p}\cdot \vec{q}=xx'+yy'+zz\text{ }\!\!'\!\!\text{ }\]
So, using this formula of dot product we will first of all find dot product of $\vec{a}\text{ and }\vec{b}$
Dot product of $\vec{a}\text{ and }\vec{b}$ is given as below:
\[\begin{align}
  & \vec{a}\cdot \vec{b}=\left( \hat{i}+3\hat{j}+7\hat{k} \right)\cdot \left( 2\hat{i}-3\hat{j}+6\hat{k} \right) \\
 & \vec{a}\cdot \vec{b}=2+3(-3)+7(6) \\
 & \vec{a}\cdot \vec{b}=2-9+42 \\
 & \vec{a}\cdot \vec{b}=44-9 \\
 & \vec{a}\cdot \vec{b}=35\text{ }.\text{ }.\text{ }.\text{ }.\text{ }.\text{ }.\text{ }.\text{ }.\text{ }.\text{ }.\text{ }.\text{ }.\text{ }(i) \\
\end{align}\]
Now, finally we will compute magnitude of vector \[\vec{b}=2\hat{i}-3\hat{j}+6\hat{k}\]
A vector \[\vec{p}=x\hat{i}+y\hat{j}+z\hat{k}\text{ }\] has its magnitude as \[\left| {\vec{p}} \right|=\sqrt{{{\left( x \right)}^{2}}+{{\left( y \right)}^{2}}+{{\left( z \right)}^{2}}}\]
Using this formula above, we have magnitude of vector $\vec{b}$ as
\[\begin{align}
  & \left| {\vec{b}} \right|=\sqrt{{{\left( 2 \right)}^{2}}+{{\left( -3 \right)}^{2}}+{{\left( 6 \right)}^{2}}} \\
 & \left| {\vec{b}} \right|=\sqrt{4+9+36} \\
 & \left| {\vec{b}} \right|=\sqrt{49} \\
\end{align}\]
Opening square root \[\left| {\vec{b}} \right|=7\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (ii)}\]
Now finally, we will use the formula of projection of vector \[\vec{a}\text{ on }\vec{b}\] which is given as $\dfrac{\vec{a}\cdot \vec{b}}{\left| {\vec{b}} \right|}$
Substituting value of $\vec{a}\cdot \vec{b}\text{ and }\left| {\vec{b}} \right|$ from equation (i) and (ii) we get:
\[\begin{align}
  & \text{Projection of}~\text{ }\vec{a}\text{ on }\vec{b}=\dfrac{35}{7} \\
 & \text{Projection of}~\text{ }\vec{a}\text{ on }\vec{b}=5 \\
\end{align}\]
Therefore, the value of projection of \[\vec{a}\text{ on }\vec{b}\text{ is 5}\].

Note: The key point to note in this question is that, at the point where we used $\left| {\vec{b}} \right|=\sqrt{49}$ and in normal cases $\left| {\vec{b}} \right|=\pm 7$ because square root always opens up with both positive and negative sign. But, here we have only taken +7 because we have $\left| {\vec{b}} \right|$ at LHS and value of mode is always positive. So, -7 is ignored. While applying the formula for projection of $\vec{a}\text{ on }\vec{b}$ we divide by magnitude of $\vec{b}$ and not $\vec{a}$ so, be careful not to make this mistake.