Question

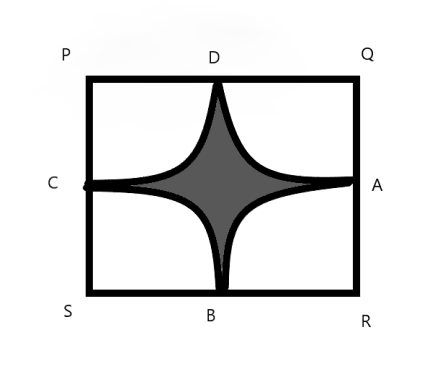
Find the area of the shaded region in the given figure where PQRS is a square of side and A, B, C, D are the midpoints of PQ, QR, RS and PS.

Answer 1

Hint:We can clearly see from the diagram that PQRS is a square of side \[{\text{12cm}}\] and four quarter circles are inscribed in it.
So , we need to calculate the area of a square and subtract the area of a four quarter circle from it.

Complete step-by-step answer:
Given the side of square as 12cm
First of all calculate the area of the square which is \[{{\text{a}}^{\text{2}}}\]where a is the side length of the square.
\[{\text{A = }}{{\text{a}}^{\text{2}}}{\text{ = (12}}{{\text{)}}^{\text{2}}}{\text{ = 144c}}{{\text{m}}^{\text{2}}}\]
Now , let us analyse any one of the quarter circle because all are similar,
So , taking \[ \odot \]DSC we can see that it’s radius is DS which is half the length of the side of a square
So , \[{\text{r = }}\dfrac{{{\text{12}}}}{{\text{2}}}{\text{ = 6cm}}\]
So area of one quarter circle is
\[
  {\text{A' = }}\dfrac{{{{\pi }}{{\text{r}}^{\text{2}}}}}{{\text{4}}}{\text{ = }}\dfrac{{{{\pi (6}}{{\text{)}}^{\text{2}}}}}{{\text{4}}} \\
  {\text{ = }}\dfrac{{{{\pi 36}}}}{{\text{4}}} \\
  {{ = 9\pi }} \\
  \]
Hence the area of all four quarter circle is
\[
  {{4A' = (4)9\pi }} \\
  {{ = 36\pi }} \\
  {{ = 113}}{\text{.04c}}{{\text{m}}^{\text{2}}} \\
  \]
Hence the area of the shaded portion is
\[
  {{ = A - 4A'}} \\
  {{ = 144 - 113}}{\text{.04}} \\
  {{ = 30}}{\text{.96c}}{{\text{m}}^{\text{2}}} \\
  \]
Thus, above is our required answer.

Note: Arcs of quarter circles are drawn inside the square. The centre of each circle is at each corner of the square.
We can say that a circle is inscribed in the square, just the four quarters are rearranged, so we can simply subtract the area of the circle from the area of the square.