Question

Find the area of the region$\left\{ \left( x,y \right):{{x}^{2}}\le y\le \left| x \right| \right\}$.

Answer 1

Hint: First draw the graph of $y={{x}^{2}}$. Now, $y\ge {{x}^{2}}$ is the region inside the parabola. Then draw the graph of $y=\left| x \right|$. Now, $y\le \left| x \right|$ is the region outside the graph $y=\left| x \right|$. To find the limits of integration, solve the equation: $x=\left| x \right|$ and determine the values of ‘x’. The smaller value of x will be the lower limit and greater value of x will be the upper limit. When we will draw the graph of these functions, we will see that it is symmetric about the y-axis. Therefore, there will be two similar regions of area, one in the 1st quadrant and the other in the 2nd quadrant. We have to determine the area of the region in the 1st quadrant and multiply it by 2 to get the total bounded area. To find the area, use the formula: $A=\int\limits_{a}^{b}{\left[ f(x)-g(x) \right]}dx$, where A is the area bounded between the curves, ‘a’ is the lower limit and ‘b’ is the upper limit. In the formula of area, f(x) is the graph of a function having higher value than the function g(x) in the range $\left[ a,b \right]$.

Complete step-by-step answer:
We have been provided with two inequalities:
$y\ge {{x}^{2}}......................(i)$
$y\le \left| x \right|.....................(ii)$
Let us solve these two equations by removing the inequality sign to determine the point of intersection.
Removing the inequality sign, we get,
$y={{x}^{2}}......................(iii)$
$y=\left| x \right|.....................(iv)$
Equating the value of ‘y’ from equation (iii) in equation (iv), we get,
$\left| x \right|={{x}^{2}}$
On squaring the two sides to remove modulus, we get,
$\begin{align}
  & {{x}^{2}}={{x}^{4}} \\
 & \Rightarrow {{x}^{4}}-{{x}^{2}}=0 \\
 & \Rightarrow {{x}^{2}}\left( {{x}^{2}}-1 \right)=0 \\
\end{align}$
Substituting each term equal to 0, we get,
$\begin{align}
  & {{x}^{2}}=0\text{ and }{{x}^{2}}-1=0 \\
 & \Rightarrow x=0\text{ and }{{x}^{2}}=1 \\
 & \Rightarrow x=0\text{ and }x=\pm 1 \\
\end{align}$
Hence, the lower limit is (x = -1) and the upper limit is (x = 1).
Let us draw the graph of the two functions.
To draw the graph of $y=\left| x \right|$, we have to consider two different situations:
\[y=\left\{ \begin{align}
  & x,\text{ }x\ge 0 \\
 & -x,\text{ }x\le 0 \\
\end{align} \right\}\].
So, we have to draw the graphs of y = x and y = -x separately.

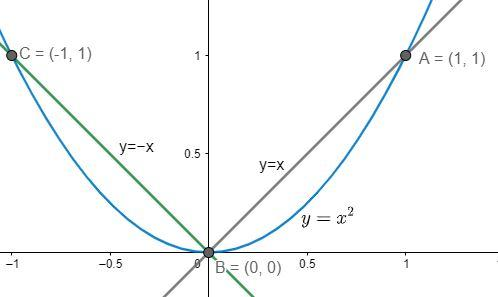
We do not have to consider the graph below x-axis as the value of y will always be positive.
Clearly we can see that the graph of the function $y=\left| x \right|$ is present above the graph of the function $y={{x}^{2}}$, in the range $\left[ -1,1 \right]$.
Therefore, $f(x)=\left| x \right|$ and $g(x)={{x}^{2}}$.
As we can see that the graph is symmetric about the y-axis, therefore, areas of the bounded regions in the two quadrants are equal. Therefore, we have to determine the area of the region in the 1st quadrant and multiply it by 2.
Now, using the formula for area of the curve bounded between the two functions: $A=2\times \int\limits_{a}^{b}{\left[ f(x)-g(x) \right]}dx$, we get,
\[A=2\times \int\limits_{0}^{1}{\left[ \left| x \right|-{{x}^{2}} \right]}dx\]
We know that, \[x\ge 0,\left| x \right|=x\]. Therefore, removing modulus sign, we get,
\[A=2\times \int\limits_{0}^{1}{\left[ x-{{x}^{2}} \right]}dx\]
Breaking the two terms, we get,
\[\Rightarrow A=2\times \left\{ \int\limits_{0}^{1}{x}dx-\int\limits_{0}^{1}{{{x}^{2}}}dx \right\}\]
Using the rule for integration given by: \[\int{{{x}^{a}}dx}=\dfrac{{{x}^{a+1}}}{a+1}\], we get,
\[\begin{align}
  & \Rightarrow A=2\times \left[ \dfrac{{{x}^{1+1}}}{1+1}-\dfrac{{{x}^{2+1}}}{2+1} \right]_{0}^{1} \\
 & \Rightarrow A=2\left[ \dfrac{{{x}^{2}}}{2}-\dfrac{{{x}^{3}}}{3} \right]_{0}^{1} \\
\end{align}\]
Substituting the limits, we get,
\[\begin{align}
  & \Rightarrow A=2\left[ \left( \dfrac{{{1}^{2}}}{2}-\dfrac{{{1}^{2}}}{3} \right)-\left( \dfrac{{{0}^{2}}}{2}-\dfrac{{{0}^{2}}}{3} \right) \right] \\
 & \Rightarrow A=2\left[ \left( \dfrac{1}{2}-\dfrac{1}{3} \right) \right] \\
 & \Rightarrow A=2\times \dfrac{1}{6} \\
 & \Rightarrow A=\dfrac{1}{3}\text{ sq}\text{. units} \\
\end{align}\]

Note: One my note that, if we do not multiply the area of one region by 2 and take the area from the limit -1 to 1, we will get the same value because of the symmetric nature of the given functions. But this will be a lengthy process because then we will have to consider more conditions and therefore, the chances of making mistakes will be high.