Question

Find the area of the region \[\left\{ \left( x,y \right):{{x}^{2}}+{{y}^{2}}\le 2ax,{{y}^{2}}\ge ax,x\ge 0,y\ge 0 \right\}\].

Answer 1

Hint: First, from the given expression / conditions, find 2 curves which we need to find the area. Next by using elimination method find the points of intersection of the curves. By looking at their equations, use normal co – ordinate geometry knowledge to find their shapes. Draw the curves together on a graph. By using their diagrams mark the area which is common in both of them. Now, integrate the curves to find the area and subtract the extra area to get the area which is in common to both curves.

Complete step-by-step answer:
Elimination method:
First write 2 curve equations which you need to solve to find intersection points. Then try to convert one variable in terms of another variable by using any one of the equations. Now substitute this variable in terms of others into the remaining equation. Now the remaining equation turns into an equation of one variable. By normal geometry find the variable. Using previous relations, find the other variable. Thus, you get the intersection point(s).
The given expressions in the question are written as:
\[{{x}^{2}}+{{y}^{2}}\le 2ax\], \[{{y}^{2}}\ge ax\], \[x,y\ge 0\]
The second curve can be directly categorized as parabola.
The curves are written as:
\[{{x}^{2}}+{{y}^{2}}=2ax\] - (1)
\[{{y}^{2}}=ax\] - (2)
By substituting equation (2) in equation (1), we get:
\[\Rightarrow {{x}^{2}}+ax=2ax\]
By subtracting 2ax on both sides of equation, we get:
\[\Rightarrow {{x}^{2}}-ax=0\]
By taking x common on L. H. S of equation, we get:
\[\Rightarrow x\left( x-a \right)=0\]
By this we can say values of x to be 0, a.
From equation (2), we can say that, \[{{y}^{2}}=ax\].
By applying square root on both sides we get:
\[\Rightarrow y=\sqrt{ax}\]
If x = 0, \[y=\sqrt{0}=0\].
If x = a, \[y=\sqrt{a.a}=\sqrt{{{a}^{2}}}\].
By considering negative roots we say, y = a, -a.
So, from these we say intersections to be (0, 0), (a, a), (a, -a).
Now subtract 2ax and add \[{{a}^{2}}\] on both sides to equation (1), we get:
\[\Rightarrow {{x}^{2}}-2ax+{{a}^{2}}+{{y}^{2}}={{a}^{2}}\], we know \[{{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\].
By substituting above identity, we get: \[{{\left( x-a \right)}^{2}}+{{y}^{2}}={{a}^{2}}\].
This is an equation of circle with radius a center at (a, 0).
The above line is simple co – ordinary geometry.
We will draw the curves on graph and mark areas.
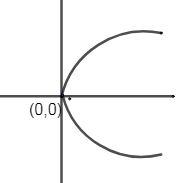
Curves: - \[{{y}^{2}}=ax\]

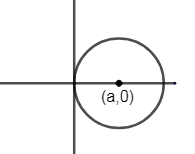
\[{{x}^{2}}+{{y}^{2}}=2ax\]

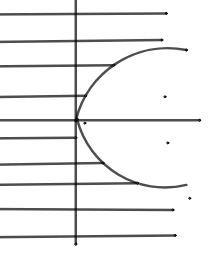
Areas: - \[{{y}^{2}}\ge ax\], \[\ge \] implies the area outside.

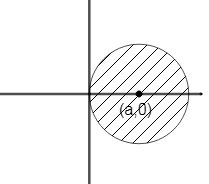
\[{{x}^{2}}+{{y}^{2}}\le 2ax\], \[\le \] implies area bounded.

Combined: -

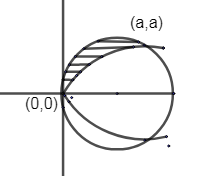
Only the upper part is considered because it is given, \[x\ge 0,y\ge 0\].
Parabola equation is given by, \[{{y}^{2}}=ax\].
Circle equation is given by, \[{{x}^{2}}+{{y}^{2}}=2ax\].
By subtracting \[{{x}^{2}}\] on both sides, we get: \[{{y}^{2}}=2ax-{{x}^{2}}\].
By applying square root to both the equations, we turn them to: -
\[\Rightarrow y=\sqrt{ax}\] - (3)
\[\Rightarrow y=\sqrt{2ax-{{x}^{2}}}\] - (4)
We know the circle lies above the parabola in the required region of area calculation.
The area between 2 curves f (x), g (x) who intersect at (\[{{x}_{1}},{{y}_{1}}\]), (\[{{x}_{2}},{{y}_{2}}\]) is given by area = \[\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{\left( f\left( x \right)-g\left( x \right) \right)dx}\], where f (x) lies above g (x).
Here we have \[f\left( x \right)=\sqrt{2ax-{{x}^{2}}};g\left( x \right)=\sqrt{ax};{{x}_{1}}=0;{{x}_{2}}=a\].
By substituting above values into area equation we get:
Area = \[\int\limits_{0}^{a}{\left( \sqrt{2ax-{{x}^{2}}}-\sqrt{a}\sqrt{x} \right)dx}\]
We know, \[2ax-{{x}^{2}}\] can be written as \[{{a}^{2}}-\left( {{x}^{2}}-2ax \right)-{{a}^{2}}={{a}^{2}}-{{\left( x-a \right)}^{2}}\].
By substituting this area turns into:
Area = \[\int\limits_{0}^{a}{\left( \sqrt{{{a}^{2}}-{{\left( x-a \right)}^{2}}} \right)dx}-\int\limits_{0}^{a}{\sqrt{ax}dx}\]
Let x – a = t in first part of area, we get: \[\left( dx=dt \right)\]
x – a = t when x = 0, t = 0 – a = -a
when x = a, t = a – a = 0
Area = \[\int\limits_{-a}^{0}{\sqrt{{{a}^{2}}-{{t}^{2}}}dt}-\int\limits_{0}^{a}{\sqrt{ax}dx}\]
By basic integration we know that,
\[\begin{align}
  & \int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx}=\dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{a}+C \\
 & \int{\sqrt{kx}dx}=\sqrt{k}\dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}}+C \\
\end{align}\]
By substituting these into area, we get it as:
Area = \[\left[ \dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{a} \right]_{-a}^{0}-\left[ \sqrt{a}\dfrac{{{x}^{\dfrac{3}{2}}}}{3}2 \right]_{0}^{a}\]
By substituting limits and subtracting them, we get it as:
Area = \[\left[ \dfrac{0}{2}\sqrt{{{a}^{2}}-0}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}0-\dfrac{\left( -a \right)}{2}\sqrt{{{a}^{2}}-{{a}^{2}}}-\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{-a}{a} \right) \right]-\left[ \dfrac{2}{3}\sqrt{a}\left( {{a}^{\dfrac{3}{2}}}-{{0}^{\dfrac{3}{2}}} \right) \right]\]
By simplifying above we get area to be as: -
Area = \[-\dfrac{{{a}^{2}}}{2}\left( \dfrac{-\pi }{2} \right)-\dfrac{2{{a}^{2}}}{3}\]
By simplifying more we can write area = \[\dfrac{\pi {{a}^{2}}}{4}-\dfrac{2{{a}^{2}}}{3}=\left( \dfrac{\pi }{4}-\dfrac{2}{3} \right){{a}^{2}}\]
Therefore area bounded by \[{{x}^{2}}+{{y}^{2}}\le 2ax,{{y}^{2}}>ax\] is \[\left( \dfrac{\pi }{4}-\dfrac{2}{3} \right){{a}^{2}}\] square units.

Note: Be careful you must take the negative root of y as it is also an intersection point. Do not take area in the \[{{4}^{th}}\] quadrant as it is given \[x\ge 0,y\ge 0\] area must be in the first quadrant students tend to confuse and take the area in \[{{4}^{th}}\] also into consideration but it is not correct.