Question

Find the area of the region $\left\{ \left( x,y \right):{{x}^{2}}+{{y}^{2}}\le 4,x+y\ge 2 \right\}.$

Answer 1

Hint: In this problem, we will find the area of the region $\left\{ \left( x,y \right):{{x}^{2}}+{{y}^{2}}\le 4,x+y\ge 2 \right\}$ by using integration. To find the area of the given region first we will calculate the area of the part of the circle which lies in the first quadrant and the triangle ABC. After finding the area of the part of the circle and triangle ABC. To find the area of the required we will subtract the area of the triangle from the area of the part of the circle in the first quadrant.

Complete step by step answer:
The image of given region is given as follows:

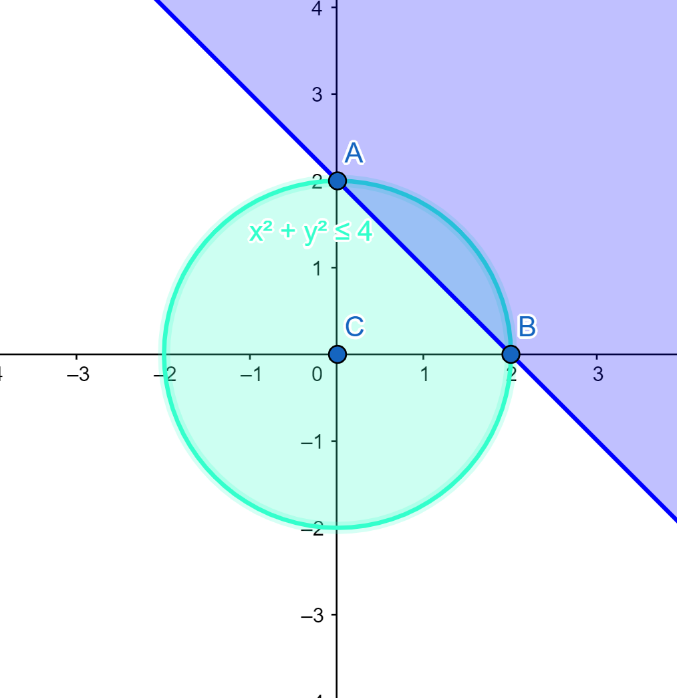
The given equation of circle is
${{x}^{2}}+{{y}^{2}}=4....(1)$
And equation of the line is
$x+y=2....(2)$
Solving equation (1) and equation (2), we get
${{x}^{2}}+{{\left( 2-x \right)}^{2}}=4$
${{x}^{2}}+4-4x+{{x}^{2}}=4$
$2{{x}^{2}}-4x=0$
$2x\left( x-2 \right)=0$
$\Rightarrow x=0\text{ or }x=2$
Let A = required area.
A1 = area of the region bounded by region ABC
A2 = area of the region bounded by$\Delta \text{ABC}$.
\[\text{A=}{{\text{A}}_{\text{1}}}-{{\text{A}}_{\text{2}}}\]
\[\text{A=}\int\limits_{\text{region ABC}}{y\text{ }dx}-\int\limits_{\text{ }\!\!\Delta\!\!\text{ ABC}}{y\text{ }dx}\]
\[\text{A=}\int_{0}^{2}{\sqrt{4-{{x}^{2}}}}dx-\int_{0}^{2}{\left( 2-x \right)dx}\]
Since, \[\int{\sqrt{{{a}^{2}}-{{x}^{2}}}}dx=\dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{x}{a} \right)+c\]
\[\text{A=}\left[ \dfrac{x}{2}\sqrt{4-{{x}^{2}}}+\dfrac{4}{2}{{\sin }^{-1}}\left( \dfrac{x}{2} \right) \right]_{0}^{2}-\left[ \dfrac{{{\left( 2-x \right)}^{2}}}{-2} \right]_{0}^{2}\]
\[\text{A=}\left( \left[ \dfrac{2}{2}\sqrt{4-{{2}^{2}}}+\dfrac{4}{2}{{\sin }^{-1}}\left( \dfrac{2}{2} \right) \right]-\left[ \dfrac{0}{2}\sqrt{4-{{0}^{2}}}+\dfrac{4}{2}{{\sin }^{-1}}\left( \dfrac{0}{2} \right) \right] \right)+\left( \left[ \dfrac{{{\left( 2-2 \right)}^{2}}}{-2} \right]-\left[ \dfrac{{{\left( 2-0 \right)}^{2}}}{-2} \right] \right)\]
\[\text{A=}\left( \left[ \dfrac{2}{2}\sqrt{4-4}+2{{\sin }^{-1}}\left( 1 \right) \right]-\left[ 0 \right] \right)+\left( \left[ 0 \right]-\left[ \dfrac{{{\left( 2 \right)}^{2}}}{-2} \right] \right)\]
\[\text{A=}\left( \left[ 0+2\left( \dfrac{\pi }{2} \right) \right] \right)+\left( \left[ \dfrac{4}{-2} \right] \right)\]
\[\text{A=}\left( \pi \right)+\left( -2 \right)\]
\[\text{A=}\pi -\text{2}\] sq. units
Area of the region \[\text{A=}\pi -\text{2}\]sq. units.

Note:
If the curve, under consideration, is below the x-axis then the bounded area by curve, x-axis and the line is negative. So we consider the absolute value of the area. The area of the portion lying above the x-axis is positive and lying below is negative. If the curve under consideration lies both above and below the x-axis, say A1>0 and A2<0, then A the area of the region is given by $\text{A=}{{\text{A}}_{\text{1}}}\text{+}\left| {{\text{A}}_{\text{2}}} \right|$. Try not to make any calculation errors.