Question

Find the area of the region bounded by the curve $y=\sqrt{x}$ and $y=x$.

Answer 1

Hint: First draw the graph of the two functions and find the intersection points by solving the two equations. Once the point is determined apply the formula for area bounded by two curves: $A=\int\limits_{a}^{b}{\left[ f(x)-g(x) \right]}dx$, where A is the area bounded between the curves, ‘a’ is the lower limit and ‘b’ is the upper limit. Here, ‘a’ and ‘b’ are the values of ‘x’, obtained after solving the equations. In the formula of area, f(x) is the graph of a function having higher value than the function g(x) in the range $\left[ a,b \right]$.

Complete step-by-step answer:
We have been provided with the two equations:
$y=\sqrt{x}.................(i)$
$y=x...................(ii)$
Let us solve these two equations to determine the point of intersection.
Equating the value of ‘y’ from equation (i) in equation (ii), we get,
$\sqrt{x}=x$
On squaring the two sides, we get,
$\begin{align}
  & x={{x}^{2}} \\
 & \Rightarrow {{x}^{2}}-x=0 \\
 & \Rightarrow x\left( x-1 \right)=0 \\
\end{align}$
Substituting each term equal to 0, we get,
x = 0 or x = 1
Hence, the lower limit is (x = 0) and the upper limit is (x = 1).
Let us draw the graph of the two functions.

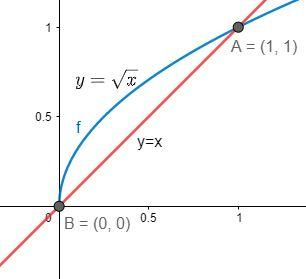
Clearly we can see that the graph of the function $y=\sqrt{x}$ is present above the graph of the function $y=x$, in the range $\left[ 0,1 \right]$.
Therefore, $f(x)=\sqrt{x}$ and $g(x)=x$.
Now, using the formula for area of the curve bounded between the two functions: $A=\int\limits_{a}^{b}{\left[ f(x)-g(x) \right]}dx$, we get,
\[\begin{align}
  & A=\int\limits_{0}^{1}{\left[ \sqrt{x}-x \right]}dx \\
 & \Rightarrow A=\int\limits_{0}^{1}{\left[ {{x}^{\dfrac{1}{2}}}-x \right]}dx \\
\end{align}\]
Breaking the two terms, we get,
\[\Rightarrow A=\int\limits_{0}^{1}{{{x}^{\dfrac{1}{2}}}}dx-\int\limits_{0}^{1}{x}dx\]
Using the rule for integration given by: \[\int{{{x}^{a}}dx}=\dfrac{{{x}^{a+1}}}{a+1}\], we get,
\[\begin{align}
  & \Rightarrow A=\left[ \dfrac{{{x}^{\dfrac{1}{2}+1}}}{\dfrac{1}{2}+1}-\dfrac{{{x}^{1+1}}}{1+1} \right]_{0}^{1} \\
 & \Rightarrow A=\left[ \dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}}-\dfrac{{{x}^{2}}}{2} \right]_{0}^{1} \\
 & \Rightarrow A=\left[ \dfrac{2{{x}^{\dfrac{3}{2}}}}{3}-\dfrac{{{x}^{2}}}{2} \right]_{0}^{1} \\
\end{align}\]
Substituting the limits, we get,
\[\begin{align}
  & \Rightarrow A=\left[ \dfrac{2\times {{1}^{\dfrac{3}{2}}}}{3}-\dfrac{{{1}^{2}}}{2} \right]-\left[ \dfrac{2\times {{0}^{\dfrac{3}{2}}}}{3}-\dfrac{{{0}^{2}}}{2} \right] \\
 & \Rightarrow A=\left[ \dfrac{2}{3}-\dfrac{1}{2} \right] \\
 & \Rightarrow A=\dfrac{4-3}{6} \\
 & \Rightarrow A=\dfrac{1}{6}\text{ sq}\text{. units} \\
\end{align}\]

Note: One my note that, we can also take the area of the region bounded as $A=\int\limits_{a}^{b}{\left[ g(x)-f(x) \right]}dx$. This expression will give the negative value of the area and we know that the area cannot be negative, therefore, after the negative numerical value is obtained, take its modulus to make it positive. Or we can say we have to calculate: $A=\left| \int\limits_{a}^{b}{\left[ g(x)-f(x) \right]}dx \right|$. This is not a process but in case you took the opposite difference of functions and got the value of area negative, don’t panic and just take its modulus.