Question

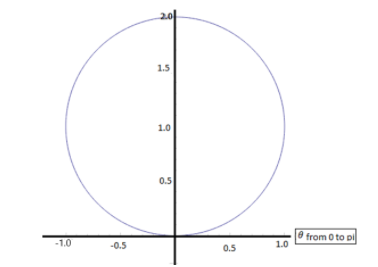
Find the area of the polar curve,$r = 2\sin \theta $ from $0 \leqslant \theta \leqslant \pi .$

Answer 1

Hint: We’ll use the formula for the area of the polar curves which is $A = \int\limits_{\theta 1}^{\theta 2} {\dfrac{1}{2}{r^2}d\theta } $, using the integration method as the limits of the variable i.e. theta is given to us.
Substituting and then simplifying the equation we’ll get the area of the polar curves.

Complete step-by-step answer:
Given data: $r = 2\sin \theta $ where $0 \leqslant \theta \leqslant \pi .$

We know that the formula for the area of a polar curve is given by
$A = \int\limits_{\theta 1}^{\theta 2} {\dfrac{1}{2}{r^2}d\theta } $
Squaring both sides of the given curve
i.e. $r = 2\sin \theta $
$ \Rightarrow {r^2} = 4{\sin ^2}\theta $
Therefore, the area of the given curve$ = \int\limits_0^\pi {\dfrac{1}{2}{r^2}d\theta } $
On Substituting the value of r, we get,
$ = \int\limits_0^\pi {\dfrac{{4{{\sin }^2}\theta }}{2}d\theta } $
$ = \int\limits_0^\pi {2{{\sin }^2}\theta d\theta } $ ………..(1)
Using the double angle formula
i.e. $\cos 2x = 1 - 2{\sin ^2}x$
now, finding the value of ${\sin ^2}x$
$2{\sin ^2}x = 1 - \cos 2x$
Dividing the equation by 2
${\sin ^2}x = \dfrac{1}{2} - \dfrac{{\cos 2x}}{2}$
On substituting the value of ${\sin ^2}x$ in (1) we get,
$ = \int\limits_0^\pi {2\left( {\dfrac{1}{2} - \dfrac{{\cos 2\theta }}{2}} \right)d\theta } $
On Simplifying the brackets, we get,
$ = \int\limits_0^\pi {(1 - \cos 2\theta )d\theta } $
Now, using \[\int\limits_\alpha ^b {(A + B)dx} = \int\limits_\alpha ^b {(A)dx} + \int\limits_\alpha ^b {(B)dx} \], we get,
$ = \int\limits_0^\pi {1d\theta } - \int\limits_0^\pi {\cos 2\theta d\theta } $
Now using \[\int\limits_\alpha ^b {{x^n}dx} = \left| {\dfrac{{{x^{n + 1}}}}{{n + 1}}} \right|_a^b\]and \[\int\limits_\alpha ^b {\cos nxdx} = \dfrac{{\left| {\sin nx} \right|_a^b}}{n}\], we get,
$ = \left| \theta \right|_0^\pi - \dfrac{{\left| {\sin 2\theta } \right|_0^\pi }}{2}$
Now on simplifying the limits, we get,
$ = \left( {\pi - 0} \right) - \dfrac{{\left( {\sin 2\pi - \sin 0} \right)}}{2}$
As, $\sin 2\pi = 0$, we get,
$ = \pi $
Hence, the area of the polar curve,$r = 2\sin \theta $ from $0 \leqslant \theta \leqslant \pi $ is $\pi $.

Note: Most of the people just integrate r with the given limits of the variable
i.e. \[A = \int\limits_\alpha ^b {rd\theta } \], but this formula is wrong and won’t lead towards the correct answer, for any of the questions so avoid using this formula directly for the area of any of the polar curves.
Let simply using this formula,
Substituting the value of r and the limits
\[ \Rightarrow A = \int\limits_0^\pi {2\sin \theta d\theta } \]
Using \[\int\limits_a^b {\sin xdx} = \left| { - \cos x} \right|_a^b\]
\[ \Rightarrow A = \left| { - 2\cos \theta } \right|_0^\pi \]
Simplifying the limits
\[ \Rightarrow A = - 2(\cos \pi - \cos 0)\]
Substituting the value of \[\cos \pi = - 1\]and \[\cos 0 = 1\]
\[ \Rightarrow A = 4\]
Therefore we can see as the results are not the same, hence this is the incorrect way to find the area of the polar curves so avoid using this formula.