Question

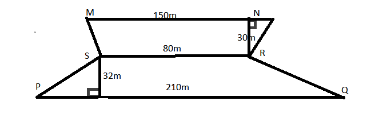
Find the area of the following field.

Answer 1

Hint: To find the area of the given field we have to divide the area in small-small well defined parts so that we can apply the basic area formulae on them and find the area and at last just aggregate them to get the final area.

Complete step-by-step answer:
Step1: Dividing the area in small parts.
We can divide the field as follows.
There are 2 trapeziums in the given field as:
PQRS and NMSR with heights as $30m$ and $30m$respectively.
We can apply the formula for the area of Trapezium as follows:
$\text{Area of trapezium}=\dfrac{a+b}{h}\times 2$
Step 2 : Finding Area of the first trapezium.
$\begin{align}
& Area=\dfrac{80+210}{32}\times 2 \\
& Area=\dfrac{290}{16}m \\
\end{align}$
Step 3: Finding the Area of the second trapezium.
$\begin{align}
& Area=\dfrac{80+150}{30}\times 2 \\
& Area=\dfrac{230}{15}m \\
\end{align}$
Step 4: Total area of the Field.
$\begin{align}
& \text{Total Area = }\dfrac{290}{16}+\dfrac{230}{15} \\
& =18.125+15.33 \\
& =33.45m \\
\end{align}$

The total area is 33.45m.

Note: This is just the one method. There are a lot other methods which can be used, one of them is rather dividing the field in 2 trapezium. We can divide them in several triangles and rectangles and then find their areas and add them up. While solving these types of questions in which we have to find the area of some large field which consists of unusual dimensions. It is recommended to divide the whole field in small parts so that we can get areas of those small well defined figures and then just add them up to get the area as a whole.