
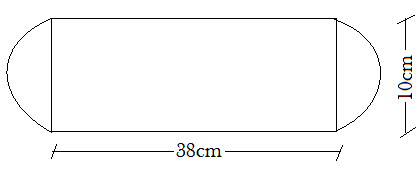
Find the area of the flower bed (with semi-circular ends) shown in the figure.
A) \[\left( {380{\text{ }} + {\text{ 12}}{\text{.5}}\pi } \right){\text{ }}c{m^2}\]
B) \[\left( {380{\text{ }} + {\text{ 10}}0\pi } \right){\text{ }}c{m^2}\]
C) \[\left( {380{\text{ }} + {\text{ }}50\pi } \right){\text{ }}c{m^2}\]
D) \[\left( {380{\text{ }} + {\text{ }}25\pi } \right){\text{ }}c{m^2}\]

Answer
581.1k+ views
Hint: The flower bed is in the shape of a rectangle with two semi-circles stuck to each of its ends. We know that the area of a rectangle with dimensions a and b is given by \[a \times b\], and area of a semicircle with radius r is given by $\dfrac{1}{2}\pi {r^2}$. The length of the rectangular part of the flower bed and the diameter of the semi-circles are given. Find the individual areas of the rectangle and the semi-circles.
Now note that the total area of the flower bed is the sum of the areas of the rectangle and the semi-circles.
Complete step-by-step answer:
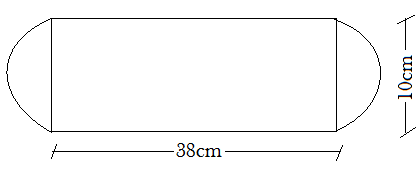
Given that, the flower bed has semi-circular ends.
Note that it contains one rectangle of dimensions \[38\;cm\; \times 10\;cm\] and two semi-circles of diameters 10 cm.
Let the length of rectangle be \[a = 38cm\] and breadth of it be \[b = 10cm\],
Also, the diameter of the semicircle is 10cm, so its radius will be \[\dfrac{{diameter}}{2} = \dfrac{{10cm}}{2} = 5cm\]
Therefore, total area of the flower bed \[ = \;area{\text{ }}of{\text{ }}rectangle\; + {\text{ }}(2 \times area{\text{ }}of{\text{ }}semicircle)\]
Now, we know that the area of a rectangle with dimensions a and b is given by \[a \times b\]
∴ the area of rectangle is $ = 38 \times 10{\text{ }} = {\text{ }}380\;c{m^2}$
Again, area of a semicircle with radius r is given by $\dfrac{1}{2}\pi {r^2}$
Therefore, area of each semicircle is $ = \dfrac{1}{2}\pi \times {5^2} = \dfrac{{25}}{2}\pi {\text{ }}c{m^2}$
∴ Area of the given figure = area of rectangle + (2×area of semi-circle)
\[ = 380 + \left( {2 \times \dfrac{{25}}{2}\pi } \right)\]
On simplification we get,
\[ = \left( {380 + 25\pi } \right)\;c{m^2}\]
Hence, the total area of the flower bed is \[\left( {380 + 25\pi } \right)\;c{m^2}\]
Hence, option D is the correct answer.
Note: Here, you should not substitute the value of \[\pi \] as in the options we can see that the area is in terms of \[\pi \], so if we substitute the value of \[\pi \] we complicate the question and get confused as then you can think that no option matches and the question is wrong.
Note that some formulae of finding the area of the following figures.
Now note that the total area of the flower bed is the sum of the areas of the rectangle and the semi-circles.
Complete step-by-step answer:

Given that, the flower bed has semi-circular ends.
Note that it contains one rectangle of dimensions \[38\;cm\; \times 10\;cm\] and two semi-circles of diameters 10 cm.
Let the length of rectangle be \[a = 38cm\] and breadth of it be \[b = 10cm\],
Also, the diameter of the semicircle is 10cm, so its radius will be \[\dfrac{{diameter}}{2} = \dfrac{{10cm}}{2} = 5cm\]
Therefore, total area of the flower bed \[ = \;area{\text{ }}of{\text{ }}rectangle\; + {\text{ }}(2 \times area{\text{ }}of{\text{ }}semicircle)\]
Now, we know that the area of a rectangle with dimensions a and b is given by \[a \times b\]
∴ the area of rectangle is $ = 38 \times 10{\text{ }} = {\text{ }}380\;c{m^2}$
Again, area of a semicircle with radius r is given by $\dfrac{1}{2}\pi {r^2}$
Therefore, area of each semicircle is $ = \dfrac{1}{2}\pi \times {5^2} = \dfrac{{25}}{2}\pi {\text{ }}c{m^2}$
∴ Area of the given figure = area of rectangle + (2×area of semi-circle)
\[ = 380 + \left( {2 \times \dfrac{{25}}{2}\pi } \right)\]
On simplification we get,
\[ = \left( {380 + 25\pi } \right)\;c{m^2}\]
Hence, the total area of the flower bed is \[\left( {380 + 25\pi } \right)\;c{m^2}\]
Hence, option D is the correct answer.
Note: Here, you should not substitute the value of \[\pi \] as in the options we can see that the area is in terms of \[\pi \], so if we substitute the value of \[\pi \] we complicate the question and get confused as then you can think that no option matches and the question is wrong.
Note that some formulae of finding the area of the following figures.
| Figure | Area |
| Square | \[{a^2}\] |
| Rectangle | \[a \times b\] |
| Triangle | $\dfrac{{{1}}}{{\text{2}}}{{ \times base \times height}}$ |
| Circle | $\pi {r^2}$ , r=radius |
| semi-circle | $\dfrac{1}{2}\pi {r^2}$ |
| Parallelogram | \[a \times h\;\] ; a =any side, h= height w.r.t that side |
| Rhombus | $\dfrac{1}{2}{d_1}{d_2}$ ; d1 and d2 are the diagonals |
Recently Updated Pages
What happens to glucose which enters nephron along class 10 biology CBSE

Write a dialogue with at least ten utterances between class 10 english CBSE

A circle is inscribed in an equilateral triangle and class 10 maths CBSE

When the JanmiKudian Act was passed that granted the class 10 social science CBSE

A sector containing an angle of 120 circ is cut off class 10 maths CBSE

The sum of digits of a two digit number is 13 If t-class-10-maths-ICSE

Trending doubts
State and prove the Pythagoras theorem-class-10-maths-CBSE

A Gulab jamun contains sugar syrup up to about 30 of class 10 maths CBSE

Distinguish between the reserved forests and protected class 10 biology CBSE

A sum of 10000 is invested at the rate of 8 per year class 10 maths CBSE

What is coalition government

Explain Whittakers System of Classification with examples class 10 biology CBSE




