Question

Find the area of a triangle whose sides are 34cm, 20cm and 42cm. Hence, find the length of altitude corresponding to the shortest side.

Answer 1

Hint: We will use the heron's formula $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ to find the area of the triangle.
Then we will substitute the values of three sides of the triangles in the formula and find the area of the triangle. Then we will use the formula $\dfrac{1}{2}\times b\times h$ for the area of the triangle to find the altitude by substituting the base as 20cm.

Complete step-by-step answer:

Let’s start solving this question.
Let’s look at the figure,

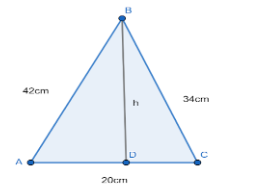
AD = h is the required altitude of the base AC.
The heron's formula is $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ .
Now we have the values of a = 34cm, b = 20cm, c = 42cm, the value of s is $\dfrac{a+b+c}{2}$
Now substituting the values of a, b, c in $\dfrac{a+b+c}{2}$ we get,
$s=\dfrac{34+20+42}{2}=48$
Now substituting the values of a, b, c and s in $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ we get,
$\begin{align}
  & Area=\sqrt{48\left( 48-34 \right)\left( 48-20 \right)\left( 48-42 \right)} \\
 & Area=\sqrt{48\times 14\times 28\times 6}=336c{{m}^{2}} \\
\end{align}$
As the shortest side is 20cm so we have take this as the base.
Now we will use the formula $\dfrac{1}{2}\times b\times h$ for area of triangle taking base as 20cm and height as h,
Hence, substituting these values we get,
$Area=\dfrac{1}{2}\times b\times h$
$\begin{align}
  & 336=\dfrac{1}{2}\times 20\times h \\
 & h=\dfrac{336}{10}=33.6cm \\
\end{align}$
Hence, the altitude corresponding to the shortest side is 33.6cm.

Note: One can also use the formula $\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}$ of cos for finding the angle, then we can use the formula of sin as $\dfrac{height}{hypotenuse}$ for the same angle to find the value of height, which is the required altitude. Hence, one can use any of the methods to find the value of altitude. One can also mistake the value of altitude as median so this point should be kept in mind.