Question

Find the area of a square, if the measure of its each diagonal is $12\text{ cm}$ .

Answer 1

Hint: In this problem we need to calculate the area of the square with a given diagonal length. First we will assume the side length of the square as $a$ , then the length of the diagonal will become $\sqrt{2}a$ . Here we will equate the given diagonal length with the value $\sqrt{2}a$ and calculate the value of side length which is $a$ by performing some basic mathematical operations. Now we will use the formula for the area of the square with given side length $a$ which is given by $A={{a}^{2}}$ . We will substitute the calculated value of $a$ in the above formula and simplify the equation to get the required result.

Complete step-by-step solution:
Given that, the diagonal length of the square is $12\text{ cm}$ .

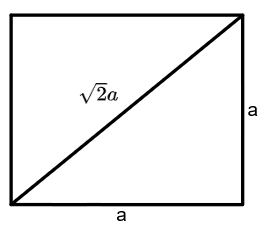
Let us assume the side length of the square as $a$. Then the diagonal length of the square will become $\sqrt{2}a$.
In the problem we have given that the diagonal length is $12\text{ cm}$. So equating the both the values, then we will have
$\sqrt{2}a=12$
Dividing the above equation with $\sqrt{2}$ on both sides, then we will get
$\begin{align}
  & \dfrac{\sqrt{2}a}{\sqrt{2}}=\dfrac{12}{\sqrt{2}} \\
 & \Rightarrow a=\dfrac{12}{\sqrt{2}} \\
\end{align}$
Now we have the side length of the square $a$ as $\dfrac{12}{\sqrt{2}}$ .
We know that the area of the square with the side length $a$ is given by $A={{a}^{2}}$.
Now the area of the square of having side length $\dfrac{12}{\sqrt{2}}$ is given by
$A={{\left( \dfrac{12}{\sqrt{2}} \right)}^{2}}$
Simplifying the above equation by using basic mathematical operations, then we will have
$\begin{align}
  & A=\dfrac{{{12}^{2}}}{{{\left( \sqrt{2} \right)}^{2}}} \\
 & \Rightarrow A=\dfrac{144}{2} \\
 & \Rightarrow A=72\text{ c}{{\text{m}}^{2}} \\
\end{align}$
Hence the area of the square with diagonal length $12\text{ cm}$ is $72\text{ c}{{\text{m}}^{2}}$ .

Note: For this problem we need not to calculate the side length of the square to find the area of the square. We have the formula for the area of the square with a given diagonal length $d$ as $A=\dfrac{{{d}^{2}}}{2}$ . We can simply use this formula to calculate the area of the square directly.