Question

Find the area of a quadrant of a circle whose radius is 7 centimeter.

Answer 1

HINT:- Before solving this question, we must know about the Quadrant of a circle.
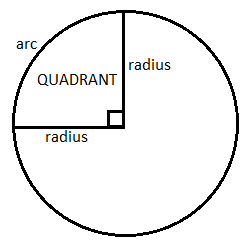
QUADRANT OF A CIRCLE: A quarter of a circle, i.e. \[\dfrac{1}{4}\] of a circle, which is made by two radiuses at right angles and the connecting arc, is called a quadrant of the circle.

Complete step-by-step answer:
Let us firstly calculate the area of the circle.
\[\begin{align}
  & =\pi {{r}^{2}} \\
 & =\dfrac{22}{7}\times 7\times 7=154c{{m}^{2}} \\
\end{align}\]
Now, as we have found the area of the circle, let us divide 154 square centimeters by 4 to find the area of the quadrant of the circle.
\[\dfrac{154\text{ }}{4}=\text{ }38.5\text{ }c{{m}^{2}}\]
Therefore, the area of the quadrant of the circle with a radius of 7 centimeter is 38.5 square cm.
NOTE:- The students must know the formula that is used in the above solution to calculate the area of a quadrant of a circle. If the students do not know the formula to calculate the area of a quadrant of a circle, then he/she will not be able to solve this question. Here is the formula:-
To calculate the area of a quadrant of a circle, we must know the area of the circle.
We know that the area of a circle is \[\pi {{r}^{2}}\] . \[\]
Now, to calculate the area of a quadrant, we need to divide the area of the circle by 4 (as four quadrants make a circle). So, we get,
Area of a quadrant, A= \[\dfrac{\left( \pi {{r}^{2}} \right)}{4}\]
Now, to find the area of a quadrant of a circle, we firstly calculate the area of the circle by the formula
\[\pi {{r}^{2}}\] and then we divide it by 4.