Question

Find the area of a circular ring formed by two concentric circles whose radii are \[5.7\text{ cm}\] and \[4.3\text{ cm }\] respectively. (Take \[\pi =3.1416\])
\[\begin{align}
  & (A)\text{ 43}\text{.98 sq}\text{.cm} \\
 & \text{(B) 53}\text{.67 sq}\text{.cm} \\
 & (C)\text{ 47}\text{.24 sq}\text{.cm} \\
 & \text{(D) 38}\text{.54 sq}\text{.cm} \\
\end{align}\]

Answer 1

Hint: We know that the area of a circle is equal to \[\pi {{r}^{2}}\] where r is the radius of the circle. We should find the area of the circle whose radius is equal to \[5.7\text{ cm}\]. Consider this area as equation (1). Now, we should find the area of the circle whose radius is equal to \[4.3\text{ cm }\text{.}\] Consider this area as equation (2). Now we should find the difference between equation (1) and equation (2). This will give the area of a circular ring formed by two concentric circles whose radii are \[5.7\text{ cm}\] and \[4.3\text{ cm }\] respectively.

Complete step-by-step solution -
Before solving the question, we should know the formula of the area of the circle. The area of the circle is equal to \[\pi {{r}^{2}}\] where r is the radius of the circle.

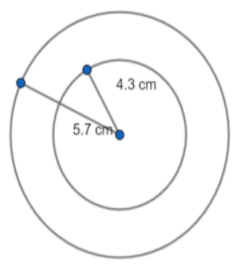
We know that the area of a circular ring is equal to the area of outer circular ring and area of inner circular ring.
From the diagram,
Area of inner circular ring = Area of circle of radius \[4.3\text{ cm }\]
Area of outer circular ring = Area of circle of radius \[5.7\text{ cm}\]
Area of circle of radius \[4.3\text{ cm }\]\[=\pi {{\left( 4.3 \right)}^{2}}=(18.49)\pi c{{m}^{2}}=(18.49)(3.1416)c{{m}^{2}}=58.088184c{{m}^{2}}......(1)\]
Area of circle of radius \[5.7\text{ cm}\]
\[=\pi {{\left( 5.7 \right)}^{2}}=(32.49)\pi c{{m}^{2}}=(18.49)(3.1416)c{{m}^{2}}=102.070584c{{m}^{2}}.....(2)\]
Now we will subtract equation (1) with equation (2).
Area of circular ring \[=(102.070584-58.088184)c{{m}^{2}}=43.9824c{{m}^{2}}\]
So, the area of the circular ring is equal to \[43.9824sq.cm\].
Hence, option (1) is correct.

Note: Students may confuse that the area of the circular ring is equal to the sum of the area of inner circle and area of outer circle. Then, we will get area of circular ring \[=(102.070584+58.088184)c{{m}^{2}}=160.158768c{{m}^{2}}\]
This is a completely wrong assumption. We should remember that the area of a circular ring is the equal difference of the area of outer circle with area of inner circle.