Question

Find the area enclosed by each of the following figure as the sum of the areas of a rectangle and a trapezium.

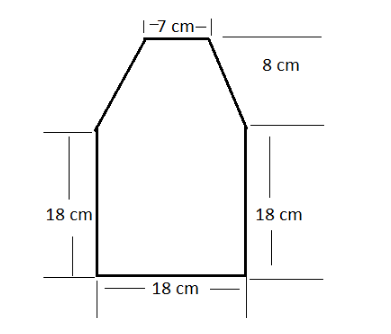
Answer 1

Hint: Here, we will re-draw the given figure, entitled with the unique alphabets and split it into two parts as the sum of the area of the rectangle and trapezium. Use the standard formula for areas of the individual and then find the total area.

Complete step-by-step answer:

Let us split the given closed figure, ABCFED in two parts –
Therefore area of ABCFED $ = $ Area of Trapezium ABCD $ + $ Area of rectangle EFCD .... (a)
Now, Area of the trapezium is $ {A_T} = \dfrac{{a + b}}{2} \times h $
Where “a” and “b” are the sides of the trapezium and “h” is the height of the trapezium.
Given that –
 $
  a = 7cm \\
  b = 18cm \\
  h = 8cm \;
  $
Place the values in the formula of area
 $ {A_T} = \left( {\dfrac{{7 + 18}}{2}} \right) \times 8 $
Simplify the above equation –
 $ {A_T} = \left( {\dfrac{{25}}{2}} \right) \times 8 $
Dividing common factors from the numerator and denominator –
 $
  {A_T} = 25 \times 4 \\
  {A_T} = 100{\text{ c}}{{\text{m}}^2}\;{\text{ }}....{\text{ (b)}} \\
  $
Now, similarly find the area of the rectangle EFCD –
Since, both the sides of the rectangle are equal, apply the formula for the area of the square.
Area of the square is the product of its two sides.
\[{A_s} = l \times l\]
Where Length of the side is, $ l = 18cm $
Place the value –
\[{A_s} = 18 \times 18\]
Simplification –
 $ \Rightarrow {A_s} = 324{\text{ c}}{{\text{m}}^2} $ ..... (c)
Place values of the equation (b) and (c) in the equation (a)-
Area of ABCFED $ = 100 + 324 $
 $ \Rightarrow Area = 424{\text{ c}}{{\text{m}}^2} $
Hence, the area of enclosed figure is $ 424{\text{ c}}{{\text{m}}^2} $
So, the correct answer is “ $ 424{\text{ c}}{{\text{m}}^2} $ ”.

Note: Remember the basic standard formulas to find the areas of the closed figures such as the quadrilaterals, square, rectangle, triangle and many more. The correct formula is most important in these types of sums. Rest do simplification carefully. Remember the rectangle with equal sides can be the square but square can never be the rectangle.