Question

How do you find the area between two curves \[y=4x-{{x}^{2}}\] and y=x?

Answer 1

Hint: This type of question is based on the concept of application of integration. We are given the two curves. To find the area enclosed by both the curves, we have to find the intersection points of both the curves. Here we find that the LHS of both the curves is equal to y. Thus, we can equate the RHS and solve the quadratic equation with respect to x. The two values of x are the limits of integration. Plot the graph of the curves \[y=4x-{{x}^{2}}\] and y=x. we find that \[y=4x-{{x}^{2}}\] is above the curve y=x. therefore, to find the area enclosed by the curves is integration of \[y=4x-{{x}^{2}}\] subtracted by the integration of the curve y=x with respect to x. do necessary calculation and find the area.\[y=4x-{{x}^{2}}\].

Complete step by step solution:
According to the question, we are asked to find the area between two curves \[y=4x-{{x}^{2}}\] and y=x.
We have been given the curves are \[y=4x-{{x}^{2}}\] and y=x. -----------(1)
First, we have to find the point of intersection between two curves.
We find that the LHS of both the curves are equal to y.
Therefore, we can equate the RHS of the both the curves.
\[\Rightarrow 4x-{{x}^{2}}=x\]
Let us subtract x from both the sides of the equation.
\[\Rightarrow 4x-{{x}^{2}}-x=x-x\]
We know that terms with same magnitude and opposite signs cancel out. On cancelling x, we get
\[4x-{{x}^{2}}-x=0\]
On further simplification, we get
\[3x-{{x}^{2}}=0\]
Let us take x common from both the terms of the equation.
\[\Rightarrow x\left( 3-x \right)=0\]
Therefore, we get
x=0 and 3-x=0
Let us consider 3-x=0.
Add x on both the sides of the equation.
\[\Rightarrow 3-x+x=0+x\]
On cancelling the common terms, we get
3=x which is x=3.
Therefore, the points of intersection with respect to x- axis are 0 and 3.
Now, we have to plot the graph of both the curves.

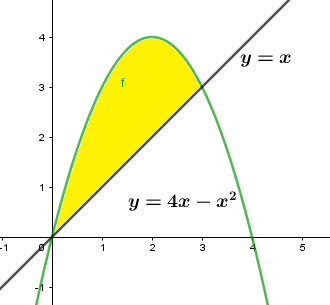
We find that the curve \[y=4x-{{x}^{2}}\]is above the curve y=x.
The shaded yellow region is the required area.
Therefore, the area can be found by integrating the curve \[y=4x-{{x}^{2}}\] and subtracting with integration of the curve y=x with respect to x.
The limits of the integration will be x=0 and x=3.
Let A be the area of the enclosed region.
\[A=\int\limits_{0}^{3}{\left( 4x-{{x}^{2}} \right)}dx-\int\limits_{0}^{3}{xdx}\]
We know that the subtraction rule of integration is \[\int{\left( u-v \right)}dx=\int{udx-\int{vdx}}\]. Using this rule, we get
\[A=\int\limits_{0}^{3}{4x}dx-\int\limits_{0}^{3}{{{x}^{2}}}dx-\int\limits_{0}^{3}{xdx}\]
\[\Rightarrow A=4\int\limits_{0}^{3}{x}dx-\int\limits_{0}^{3}{{{x}^{2}}}dx-\int\limits_{0}^{3}{xdx}\]
On further simplification, we get
\[A=3\int\limits_{0}^{3}{x}dx-\int\limits_{0}^{3}{{{x}^{2}}}dx\]
Using the power rule of integration that is \[\int{{{x}^{n}}}dx=\dfrac{{{x}^{n+1}}}{n+1}\], we get
\[\int{xdx=\dfrac{{{x}^{1+1}}}{1+1}}\]
On further simplification, we get \[\int{xdx=\dfrac{{{x}^{2}}}{2}}\].
And \[\int{{{x}^{2}}dx=\dfrac{{{x}^{2+1}}}{2+1}}\].
\[\Rightarrow \int{{{x}^{2}}dx=\dfrac{{{x}^{3}}}{3}}\]
On substituting these values to find the area, we get
\[A=3\left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{3}-\left[ \dfrac{{{x}^{3}}}{3} \right]_{0}^{3}\]
Let us now, substitute the limits to the variable x of the integral.
\[\Rightarrow A=3\left[ \dfrac{{{3}^{2}}}{2}-0 \right]-\left[ \dfrac{{{3}^{3}}}{3}-0 \right]\]
On further simplification, we get
\[A=3\times \dfrac{{{3}^{2}}}{2}-\dfrac{{{3}^{3}}}{3}\]
\[\Rightarrow A=\dfrac{{{3}^{3}}}{2}-\dfrac{{{3}^{3}}}{3}\]
We find that \[{{3}^{3}}\] is common in both the terms of the RHS. On taking \[{{3}^{3}}\] common, we get
\[A={{3}^{3}}\left( \dfrac{1}{2}-\dfrac{1}{3} \right)\]
Let us take the LCM of 2 and 3.
\[\Rightarrow A={{3}^{3}}\left( \dfrac{3-2}{6} \right)\]
On further simplification, we get
\[A={{3}^{3}}\left( \dfrac{1}{6} \right)\]
We can write the expression as
\[A={{3}^{2}}\times 3\left( \dfrac{1}{2\times 3} \right)\]
We find that 3 are common in the numerator and denominator of the RHS. On cancelling 3, we get
\[A={{3}^{2}}\left( \dfrac{1}{2} \right)\]
\[\Rightarrow A=\dfrac{{{3}^{2}}}{2}\]
We know that the square of 3 is 9.
\[\therefore A=\dfrac{9}{2}\] square units.
Therefore, the area between two curves \[y=4x-{{x}^{2}}\] and y=x is \[\dfrac{9}{2}\] sq. units.

Note: We have to use definite integrals to solve these types of questions. We can find the area by integrating both the curves with respect to y also. We have to find the point of intersection with respect to y to solve by that method. Avoid calculation mistakes based on sign convention. We should not forget to put units after finding the area without which the answer is incomplete.