Question

How do you find the area between two curves using integrals?

Answer 1

Hint: This type of question is based on the concept of application of definite integral. We first have to consider both the curves. Do necessary calculations in both the curves so that we get the value of y with respect to x. then, we have to equate both the curves. On solving the equation with variable x, we get the point of intersection of both the curves with respect to x-axis. And then plot the graph of both the equations. Observe the graph and find the curve which lies above the other curve. Integrate the above curve first subtracted by the integral of the second curve with the limits. Do necessary calculations and find the value of the area which is the required answer.

Complete step by step solution:
According to the question, we are asked to find the area between two curves.
Let us consider \[{{C}_{1}}\] and \[{{C}_{2}}\] to be both the curves where the variables are x and y.
Now, we have to make certain calculations in both the curves such that we get y in both the sides of the LHS and all the x terms in the RHS.
We know that, when two equations have same LHS, then the RHS of the equation will also be equal.
On equating the RHS, we get an equation with x as the variable.
Now, we have to find the point of intersection of both the curves \[{{C}_{1}}\] and \[{{C}_{2}}\].
Solve the obtained equation with respect to x and find the value of x.
Let us assume a and b to be the obtained values of x on solving the equation.
The points a and b with respect to x is the point of intersection of both the curves \[{{C}_{1}}\] and \[{{C}_{2}}\].
We can consider these points a and b to bet the limits of the definite integral.
Now, the area enclosed by both the curves \[{{C}_{1}}\] and \[{{C}_{2}}\] is to be found in the interval a to b.
We have to first plot the graph of both the curves.
We can understand with an example.
Let us assume \[{{C}_{1}}\] to be an upper parabola and \[{{C}_{2}}\] to be a straight line.
On plotting the graph, we get

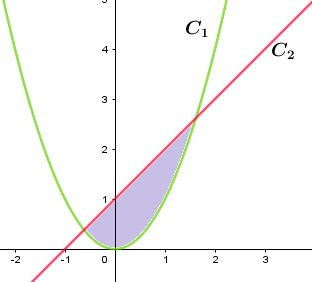
We are supposed to find the area of the shaded region.
Here, we find that the curve \[{{C}_{2}}\] is above the curve \[{{C}_{1}}\].
Therefore, to find the area, we have to subtract the integral of curve \[{{C}_{2}}\] from the integral of curve \[{{C}_{1}}\].
The formula for find the area bounded by a curve is \[A=\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{ydx}\], where \[{{x}_{1}}\] and \[{{x}_{2}}\] are the limits of the integral. Here, we have found that the limits of the integral is a and b which are the points of intersection with respect to the x-axis.
Therefore, the area enclosed by both the curves is
\[A=\int\limits_{a}^{b}{\left( {{y}_{2}}-{{y}_{1}} \right)}dx\]
Here, \[{{y}_{2}}\] is the value of y in curve \[{{C}_{2}}\] and \[{{y}_{1}}\] is the value of y in curve \[{{C}_{1}}\] with respect to x.
Integrate the functions and substitute the limits to the variable x.
Finally, we have to put the units to the answer.

Note: We have to use definite integrals to solve these types of questions. We can also find the answer by integrating with respect to y. If the final answer is negative, we have to take the magnitude only since the area can never be negative.