Question

How do you find the area between the function \[f\left( x \right)=\cos x\ \]and the x-axis on the interval \[x\in \left[ 0,2\pi \right]\]?

Answer 1

Hint: In order to find the area between the given curve \[f\left( x \right)=\cos x\ \]and the x-axis on the interval \[x\in \left[ 0,2\pi \right]\], we need to subtract the area below the upper curve and the area underneath the lower curve. We can solve this question or find the area by calculating the difference between the definite integrals of two functions. First we need to draw or plot the graph of the function by considering the given interval. Then simplify the calculus of an integral without any meaning of area by using the method i.e. \[\int_{a}^{b}{f\left( x \right)}=F\left( b \right)-F\left( a \right)\]. In this way we will get the area between the function \[f\left( x \right)=\cos x\ \]and the x-axis on the interval \[x\in \left[ 0,2\pi \right]\].

Complete step-by-step answer:
We have given that,
 \[f\left( x \right)=\cos x\ \]and the x-axis on the interval \[x\in \left[ 0,2\pi \right]\]
Using the definition of definite integral has to be used;
 \[\int_{a}^{b}{f\left( x \right)}=F\left( b \right)-F\left( a \right)\]
Now,
We have to make the graph of the function,
 \[f\left( x \right)=\cos x\ \]
And the x-axis on the interval \[x\in \left[ 0,2\pi \right]\].
The graph is as follows;

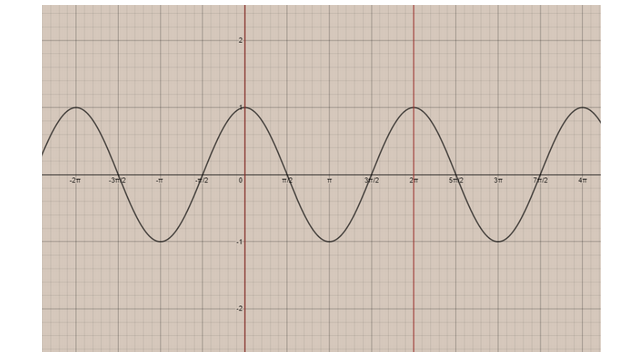
Now,
We can observe that,
In the interval \[\left[ 0,\dfrac{\pi }{2} \right]\] the graph lies over the x-axis, but in the interval \[\left[ \dfrac{\pi }{2},\dfrac{3\pi }{2} \right]\] the graph is under the x-axis.
Now,
Calculating the definite integral;
 \[A=\int_{0}^{\dfrac{\pi }{2}}{cosx dx}-\int_{\dfrac{\pi }{2}}^{\dfrac{3\pi }{2}}{cosxdx}+ \int_{\dfrac{3\pi }{2}}^{2\pi }{cosx dx}\]
Now,
We know that the property of definite integral i.e. \[\int_{a}^{b}{f\left( x \right)}=-\int_{b}^{a}{f\left( x \right)}\]
 \[A=\int_{0}^{\dfrac{\pi }{2}}{cosx dx}+\int_{\dfrac{3\pi }{2}}^{\dfrac{\pi }{2}}{cosxdx}+ \int_{\dfrac{3\pi }{2}}^{2\pi }{cosx dx}\]
Applying the rules of integration i.e. \[\int{\cos x}=\sin x+C\]
We will obtain,
 \[A=\left[ \sin x \right]_{0}^{\dfrac{\pi }{2}}+\left[ \sin x \right]_{\dfrac{3\pi }{2}}^{\dfrac{\pi }{2}}+\left[ \sin x \right]_{\dfrac{3\pi }{2}}^{2\pi }\]
Now,
 \[A=\sin \dfrac{\pi }{2}-\sin 0+\sin \dfrac{\pi }{2}-\sin \dfrac{3\pi }{2}+\sin 2\pi -\sin \dfrac{3\pi }{2}\]
Substituting the values of sine function, we will get
 \[A=1-0+1-\left( -1 \right)+0-\left( -1 \right)\]
Solving the numbers, we will get
 \[A=4\]units
Therefore,
The area between the function \[f\left( x \right)=\cos x\ \]and the x-axis on the interval \[x\in \left[ 0,2\pi \right]\] is 4 units.
Hence, this is the required answer.

Note: These types of questions are generally based on the concepts of definite integrals. While solving these types of questions, we have to use the definite integrals to solve the questions. We can also find the answer by integrating with respect to y. If the final answer is negative, then we have to take the magnitude only since the area can never be negative.