Question

Find the area and perimeter of a square plot of land, the length of whose diagonal is 15 meters. Give answers correct to 2 places of decimals.
(a) 110.50 sq. m and 40.43 m
(b) 115.50 sq. m and 45.43 m
(c) 112.50 sq. m and 42.43 m
(d) 113.50 sq. m and 43.43 m

Answer 1

Hint: We are given the length of the diagonal of the square so, first we will try to find the length of the side of the square by applying Pythagoras theorem in a right angled triangle formed by two of its sides and one of its diagonal. After that we will apply the formulas $ {{(side)}^{2}}\,and\,(4\times side) $ to find the area and perimeter of the square respectively.

Complete step-by-step answer:
We are given that the length of the diagonal(d) is 15 m.
We will suppose the side of the given square as x,

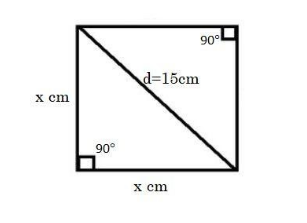
Now, we will apply the Pythagoras theorem in the lower triangle of square as shown in figure because triangle formed is a right angled triangle as angle made at all four corners by sides of square is $ {{90}^{\circ }} $ , and
We know, Pythagoras theorem states that, for a right angled triangle
 $ {{(hypotenuse)}^{2}}={{(base)}^{2}}+{{(height)}^{2}} $
So, we get
 $ {{d}^{2}}={{x}^{2}}+{{x}^{2}} $
 $ {{15}^{2}}=2{{x}^{2}} $
 $ {{x}^{2}}=\dfrac{225}{2} $
\[\begin{align}
  & {{x}^{2}}=112.5 \\
 & x=\sqrt{112.5} \\
 & x=\pm 10.61 \\
\end{align}\]
But we know that length cannot be negative, so
 $ x=10.61 $
Hence length of the side of the square is 10.61 m
Now to find the Area(A) of the square we will use the formula,
 $ A={{\left( side \right)}^{2}} $
Hence,
 $ \begin{align}
  & A={{\left( x \right)}^{2}} \\
 & A={{\left( 10.61 \right)}^{2}} \\
 & A=112.50 \\
\end{align} $
Hence area of the square is 112.50 sq. m
Now to find the Perimeter(P) of the square we will use the formula,
 $ P=4\times side $
Hence,
 $ \begin{align}
  & P=4\times x \\
 & P=4\times 10.61 \\
 & P=42.43 \\
\end{align} $
Hence perimeter of the square is 42.43 m
So, the correct answer is “Option C”.

Note: In this question while doing the calculation you need to be extra cautious as calculations involve decimals, and given options are very close to each other so be cautious.
This question can also be done by checking the values of option like we can divide perimeter of each option by 4 which will give us the length of side of the square and then we will find the length of diagonal by using Pythagoras theorem and if it matches with given diagonal length then it is right answer as all of the given perimeters in options are different we do not need to check length of diagonal through area given in options.
But we do not recommend you to do it by the method told above as it involves even more calculations just do it the way it is shown in detail.