Question

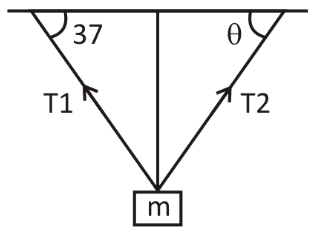
Find the angle \[\theta \] if \[{T_2} = 2{T_1}\].

A. \[{\operatorname{Cos} ^{ - 1}}\left( {\dfrac{2}{5}} \right)\]
B. \[{\operatorname{Cos} ^{ - 1}}\left( {\dfrac{1}{5}} \right)\]
C. \[{\operatorname{Cos} ^{ - 1}}\left( {\dfrac{1}{3}} \right)\]
D. none of these

Answer 1

Hint: Tension is described as the pulling force which is transmitted axially by means of string, cable etc. It is just the intermolecular force that exists inside the ropes and strings.Moreover, tension can be defined as an action-reaction pair of forces acting at each end of the said elements. While considering a rope, the tension force is felt by every section of the rope in both the directions, apart from the endpoints.

Formula used:
For two different tensions-
\[{T_2} = \dfrac{{mg\operatorname{Cos} \alpha }}{{\operatorname{Sin} (\alpha + \beta )}}\], \[{T_1} = \dfrac{{mg\operatorname{Cos} \beta }}{{\operatorname{Sin} ({{37}^ \circ } + \alpha )}}\]
Here ${T_1}$ and ${T_1}$ both are tensions that are acting on the object (as shown), $m$ is the mass of the given object, $g$ is the acceleration due to gravity and $\alpha$ ,$\beta$ are the interior angle.

Complete step by step answer:
As we know that there will be two tensions\[({T_1}\& {T_2})\] in the string due to mass m(as shown). Also one condition is given, \[{T_2} = 2{T_1}\]. We have formula for finding the tension, so
\[{T_2} = \dfrac{{mg\operatorname{Cos} \alpha }}{{\operatorname{Sin} (\alpha + \beta )}}\]
Here β is given and also T2 is tension in the second string which is given. Substitute the given values, we get-
\[2{T_1} = \dfrac{{mg\operatorname{Cos} \alpha }}{{\operatorname{Sin} ({{37}^ \circ } + \alpha )}}\] --- (1)
Now, \[{T_1} = \dfrac{{mg\operatorname{Cos} \beta }}{{\operatorname{Sin} ({{37}^ \circ } + \alpha )}}\]
\[{T_1} = \dfrac{{mg\operatorname{Cos} {{37}^ \circ }}}{{\operatorname{Sin} ({{37}^ \circ } + \alpha )}}\]--- (2)
Now, divide equation (2) by equation (1), we get-
\[\dfrac{{2{T_1}}}{{{T_1}}} = \dfrac{{\dfrac{{mg\operatorname{Cos} \alpha }}{{\operatorname{Sin} ({{37}^ \circ } + \alpha )}}}}{{\dfrac{{mg\operatorname{Cos} {{37}^ \circ }}}{{\operatorname{Sin} ({{37}^ \circ } + \alpha )}}}}\]
\[\Rightarrow 2 = \dfrac{{\operatorname{Cos} \alpha }}{{\operatorname{Cos} {{37}^ \circ }}}\]--- (3)
As we know value of \[\operatorname{Cos} {37^ \circ } = \dfrac{4}{5}\]
Now, substitute in equation (3),
We get-
\[\Rightarrow 2 = \dfrac{{\operatorname{Cos} \alpha }}{{\left( {\dfrac{4}{5}} \right)}}\]
\[\Rightarrow 2 \times \dfrac{4}{5} = \operatorname{Cos} \alpha \]
\[\Rightarrow\dfrac{8}{5} = \operatorname{Cos} \alpha \]
\[\therefore\alpha = {\operatorname{Cos} ^{ - 1}}\left( {\dfrac{8}{5}} \right)\]
So, angle is, \[\alpha = {\operatorname{Cos} ^{ - 1}}\left( {\dfrac{8}{5}} \right)\]. But it is not matching with the given options.

So, Option D will be correct.

Note:While we consider a rope, then the tension force is felt by every section of the rope in both the It is a pulling force not a pushing force. Sometimes we often draw the force of tension in the wrong direction by considering the tension a pushing force. So, it is very important to remember that tension can only pull the object but not push against it.