Question

How do I find the angle between the line and its reflection in a plane?

Answer 1

Hint: This question requires knowledge of planes topic in mathematics. We need to find the angle between the line and its reflection in a plane which can be done by first defining the incident angle or input angle and then defining the reflected angle or output angle. Then we calculate this for the given line and add both the incident and reflected angles to get the angle between the line and its reflection in a plane.

Complete step-by-step answer:
We are required to find the angle between the line and its reflection in a plane. For this, we first define what incident and reflected angles are. Let us assume a plane defined by the edges A and B which lies perpendicular to the sheet inwards. Let us also consider a plane perpendicular to this plane as shown in the figure.

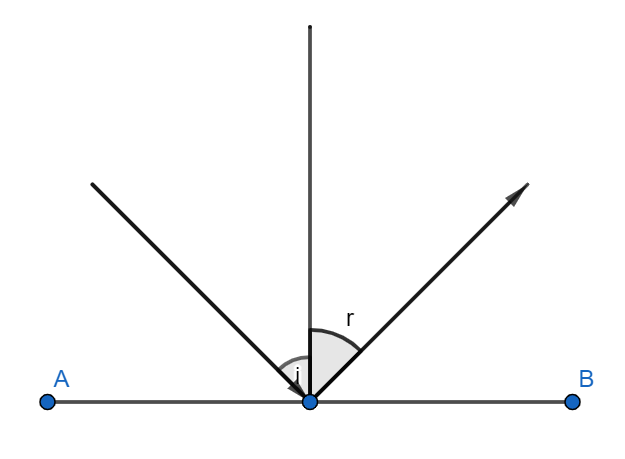
Now we show an incident line which is incident towards the intersection line of the two planes. We mention line since the intersection of two planes produces a line. Now if we measure the angle between the incident line and the perpendicular plane, we get an angle called as the incident angle or input angle. This angle defines the inclination of the incident wave towards the perpendicular plane. This is indicated by the symbol i.
If this line is now reflected through the perpendicular plane, we get another line on the right side of the perpendicular plane as shown. This line is the reflected or outgoing line. Now if we measure the angle between the reflected line and the perpendicular plane, we get an angle called as the reflected angle or output angle. This angle defines the inclination of the reflected wave towards the perpendicular plane. This is indicated by the symbol r.
We need to note that the incident angle i is usually equal to the reflected angle r since this follows the laws of reflection from physics. Therefore,
$\Rightarrow i=r$
Therefore, the angle between the line and its reflection in a plane is the sum of both the incident and reflected angles between the two lines.
$\Rightarrow i+r$
But we know that $i=r.$ Therefore,
$\begin{align}
  & \Rightarrow i+i \\
 & \Rightarrow 2i \\
\end{align}$
Hence, the angle between the line and its reflection in a plane is $2i,$ which is same as $2r.$

Note: To answer this question, students are required to go through the laws of reflection thoroughly. Another method to solve this question is to take the angle between the incident line and the AB plane and subtract this value from 90 degrees to find the angle between the incident line and the perpendicular plane. This is same as the incident angle and the remaining steps are same as in the solution.